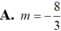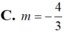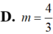Đáp án A
Gọi M( 2+2t; 1+ mt) là điểm tùy ý thuộc ∆2
Để M nằm trên ∆1 khi và chi khi:
2( 2+ 2t) -3( 1+ mt) - m= 0 hay t( 4-3m) + 1- m= 0 n(*) luôn đúng với mọi t.
∆ 1 ≡ ∆ 2 ⇔ ( * ) thỏa với mọi t ⇔ 4 - 3 m = 0 1 - m = 0 (vô nghiệm)
Vậy không có m thỏa yêu cầu bài toán.
Với giá trị nào của m thì hai đường thẳng d 1 : x = 2 + 2 t y = 1 + m t và d2 : 4x – 3y + m= 0 trùng nhau ?
A.m= 1
B.m= -1
C.m= 2
D.không có m thỏa mãn
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B.m=0.
C.m=2.
D.m=1.
Cho đường thẳng (d) :y=(m+1)x+m
câu 1 : giá trị m để đường thẳng (d) song song với đường thẳng (d1):y=2x+3
A:m=1 B:m=2 C:m=3 D: không có giá trị m
câu 2 : giá trị m để đường thẳng (d) trùng với đường thẳng (d2) y=x+3
A:m=1 B:m=2 C:m=0 D: không có giá trị m
câu 3 : giá trị m để đường thẳng (d) vuông góc với đường thẳng (d3) y=x+3
A:m=-1 B:m=-2 C:m=0 D: không có giá trị m
câu 4 : giá trị m để đường thẳng (d) cắt Parabol (P) y=x2 tại một điểm
A:m=1 B:m=2 C:m=3 D: không có giá trị m
câu 5 : giá trị m để đường thẳng (d) cắt Parabol (P) y=x2 tại hai điểm phân biệt có hoành độ x1, x2 thỏa x12+ x22= 1
A:m=1 B:m=2 C:m=3 D: không có giá trị m
Với giá trị nào của m thì hai đường thẳng d1: 4x -3y + 3m= 0 và d 2 : x = 1 + 2 t y = 4 + m t trùng nhau ?
Với giá trị nào của m thì hai đường thẳng d1: 2x- 3y -10= 0 và d 2 : x = 2 - 3 t y = 1 - 4 m t vuông góc nhau ?
Với giá trị nào của m thì hai đường thẳng (d1 ) : x−my = 0,(d2 ) :mx− y =m+1 trùng nhau ?
A. m = 0. B. m khác 1. C. m = 0 hoặc m = −1. D. m = −1.
với giá trị nào của m thì hai đường thẳng d1:2x+y+4-m=0 và d2:(m+3)x+y+2m-1=0
Với giá trị nào của m thì hai đường thẳng d1: 2x - 3y + 1 = 0 và d 2 : x = 1 + 2 t y = 7 - m t vuông góc với nhau?
A. m = 3 2
B. m = 3
C. m = -3
D. m = - 3 2
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B m=0.
C.m=2.
D.m=1.
