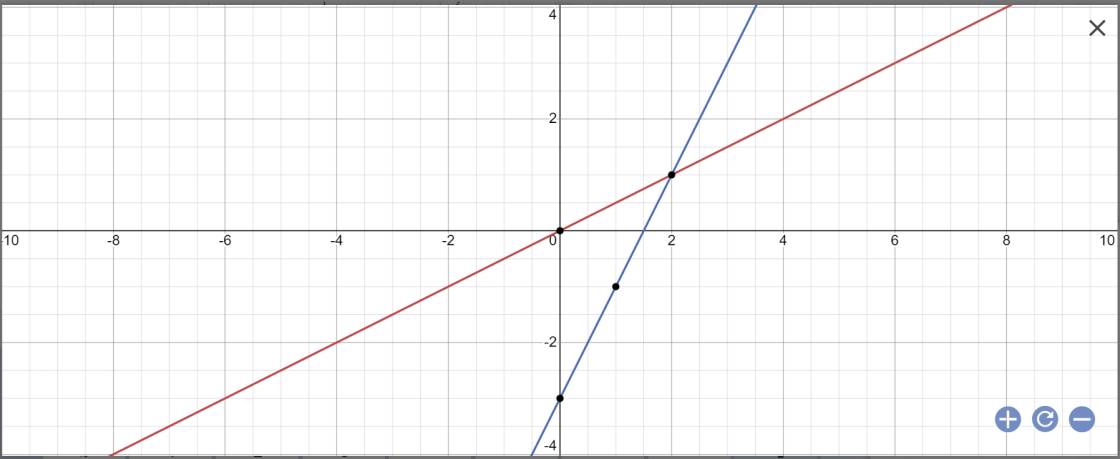
Câu 1: Trên cùng một hệ trục tọa độ Oxy cho các đường thẳng Điểm A có tọa độ là:? | ||||
|

Những câu hỏi liên quan
Cho ba đường thẳng (d1) y=\(\dfrac{1}{2}\)x-3; (d2) y=3-2x; (d3) y=-\(\dfrac{7}{6}\)x+1
a, Vẽ các đường thẳng trên cùng một hệ trục tọa độ Oxy. Chứng minh ba đường thẳng này đồng quy
b, Gọi giao điểm của 3 đường thẳng (d1); (d2); (d3) là A. Giao của (d1); (d2) với trục tung lần lượt là B và C. Tính chu vi và diện tích của tam giác ABC.
Trong mặt phẳng tọa độ Oxy Cho hàm số y = 2 x - 3 có đồ thị là đường thẳng d1 và hàm số y = 1/2 x có đồ thị là đường thẳng d2 a vẽ đồ thị d1 và d2 trên cùng hệ trục tọa độ
Câu 2
a, vẽ trên cùng hệ trục tọa độ Oxy các đồ thị hàm số sau
y=x(d1) ; y=3x(d2) ; y=-x+4(d3)
b đg thẳng d3 cắt d1,d2 lần lượt tại M,N. TÌm tọa độ điểm M và N. Tính SOMN
b: Phương trình hoành độ giao điểm của (d1) và (d3) là:
x=-x+4
hay x=2
Thay x=2 vào (d1), ta được:
y=2
Vậy: M(2;2)
Phương trình hoành độ giao điểm của (d2) và (d3) là:
3x=-x+4
hay x=1
Thay x=1 vào (d2), ta được:
y=3x1=3
Vậy: N(1;3)
Đúng 1
Bình luận (0)
Cho hai đường thẳng :
(d1): y = 1/2x + 2 và (d2): y = -x + 2
1. Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy.
2. Gọi A và B lần lượt là giao điểm của (d1) và (d2) với trục Ox , C là giao điểm của (d1) và (d2) .
Tính chu vi và diện tích của tam giác ABC (đơn vị trên hệ trục tọa độ là cm)
(d1): y = 1/2x + 2
và (d2): y = -x + 2
1. Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy.
(d1) là đường thẳng đi qua hai điểm (0; 2) và (-4; 0)
(d2) là đường thẳng đi qua hai điểm (0; 2) và (2;0)
2. Tính chu vi và diện tích của tam giác ABC
(d1) và (d2) cùng cắt nhau tại một điểm trên trục tung có tung độ bằng 2
Áp dụng định lý Pi ta go cho các tam giác AOC và BOC vuông ở O ta được:
\(AC=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}\)
\(BC=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)
Chu vi tam giác ABC : AC + BC + AB= 2√5 + 2√2 + 6
≈ 13,30
Diện tích tam giác ABC
\(\frac{1}{2}.OC.AB=\frac{1}{2}.2.6=6CM^2\)
NHÉ THAK NHÌU
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng (d1): y -1/3x và (d2): y 3x-2.1)Vẽ (d1) và (d2) trên cùng hệ trục.2) Bằng phép tính tìm tọa độ giao điểm của (d1) và (d2).3) Cho đường thẳng (d3): yax+b. Xác định a và b biết (d3) song song với (d2) và cắt (d1) tại điểm có hoành độ bằng 2.Giup minh voi a!
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng (d1): y = -1/3x và (d2): y = 3x-2.
1)Vẽ (d1) và (d2) trên cùng hệ trục.
2) Bằng phép tính tìm tọa độ giao điểm của (d1) và (d2).
3) Cho đường thẳng (d3): y=ax+b. Xác định a và b biết (d3) song song với (d2) và cắt (d1) tại điểm có hoành độ bằng 2.Giup minh voi a!
Cho hai hàm số: y = 2x – 3 và y = (-1/2)x + 2 có đồ thị lần lượt là các đường thẳng (d1) và (d2). a) Vẽ trên cùng một hệ trục tọa độ các đường thẳng (d1) và (d2). b) Tìm tọa độ giao điểm hai đường thẳng (d1) và (d2) bằng phép toán. c) Tính góc tạo bởi đường thẳng (d1) và trục Ox.
Bài 1: Cho (d1): y = 3x + 2 (d2): y = x – 2 a) Tìm tọa độ giao điểm của (d1) và (d2) với trục hoành b) Tìm tọa độ giao điểm của (d1) và (d2) với trục tung c) Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy d) Tìm tọa độ giao điểm của (d1) và (d2)
\(b,\) PT hoành độ giao điểm: \(3x+2=x-2\Leftrightarrow x=-2\Leftrightarrow y=-4\Leftrightarrow A\left(-2;-4\right)\)
Vậy \(A\left(-2;-4\right)\) là tọa độ giao điểm
Đúng 1
Bình luận (0)
Cho hàm số y=-2x-2 có đồ thị là đường thẳng d1 A/ viết phương trình đường thẳng d2 biết rằng d2 đi qua điểm M (2;-2) và song song với đường thẳng d1 B/ vẽ d1 và d2 trên cùng một hệ trục tọa độ Oxy C/ cho hàm số y= x+m có đồ thị là đường thẳng d3, xác định tham số m để đường thẳng d1 cắt đường thẳng d3 trên trục Ox
a) \(\left(d_1\right):y=-2x-2\)
\(\left(d_2\right):y=ax+b\)
\(\left(d_2\right)//d_1\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left(d_2\right):y=-2x+b\)
\(M\left(2;-2\right)\in\left(d_2\right)\Leftrightarrow-2.2+b=-2\)
\(\Leftrightarrow b=2\) \(\left(thỏa.đk.b\ne-2\right)\)
Vậy \(\left(d_2\right):y=-2x+2\)
b) \(\left\{{}\begin{matrix}\left(d_1\right):y=-2x-2\\\left(d_2\right):y=-2x+2\end{matrix}\right.\)
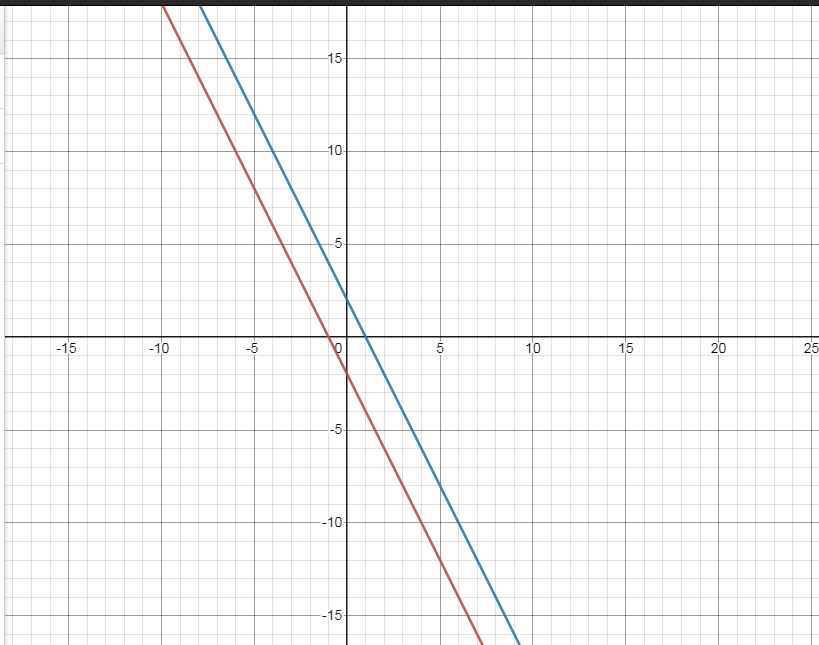
c) \(\left(d_3\right):y=x+m\)
\(\left(d_1\right)\cap\left(d_3\right)=A\left(x;0\right)\Leftrightarrow\left\{{}\begin{matrix}y=x+m\\y=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=x+m\\0=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\x=-1\end{matrix}\right.\)
\(\Rightarrow\left(d_3\right):y=x+1\)
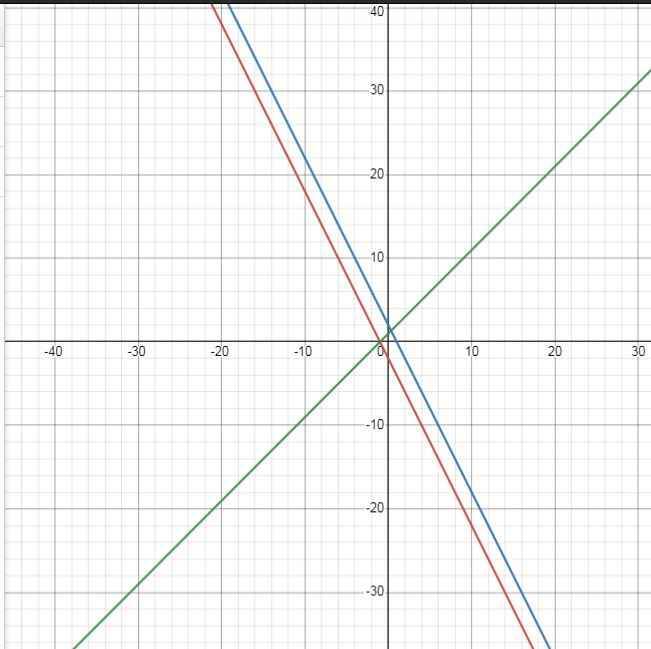
Đúng 1
Bình luận (0)
Cho hàm số y=3x-1 có đồ thị d1 và hàm số y=-x +3 có đồ thị d2 A. Vẽ đồ thị hs trên cùng hệ trục tọa độ Oxy B. Gọi giao điểm d1, d2 với trục Õ lần lượt là A và B, giao điểm của 2 đường thẳng d1 và d2 là C. Tìm tọa độ các điểm A,B,C C. Tính số đo của góc tạo bởi đường thẳng d1 với tia Ox
a: 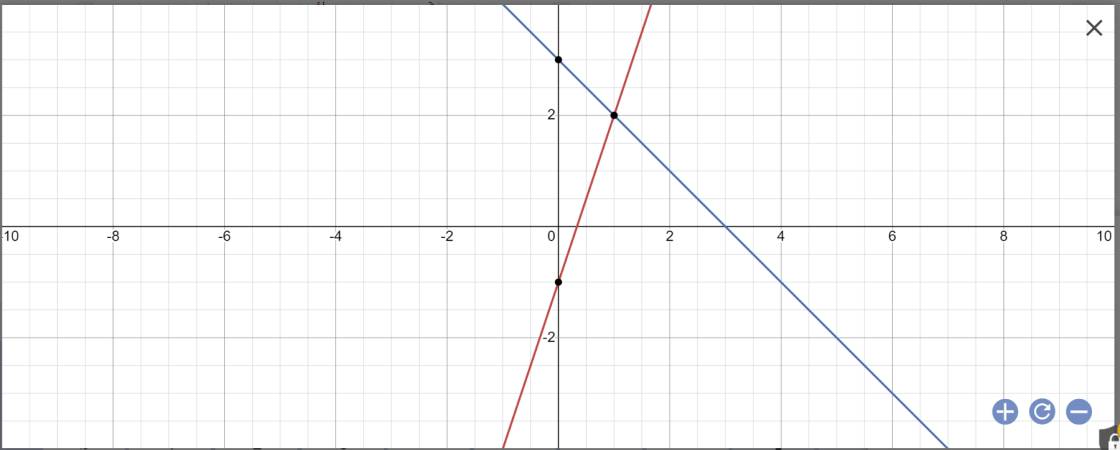
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
Đúng 0
Bình luận (0)