\(v_o=72\left(km/h\right)=20\left(m/s\right)\)

\(v=0\left(khi.dừng.lại\right)\)

\(t=\Delta t=1\left(phút\right)=60\left(s\right)\)

a) Gia tốc đoàn tàu :

\(a=\dfrac{v-v_o}{\Delta t}=\dfrac{0-20}{60}=-\dfrac{1}{3}\left(m/s\right)\)

b) Quãng đường trong chuyển động thẳng biến đổi đều:

\(s=v_ot+\dfrac{1}{2}at^2=20.60+\dfrac{1}{2}.\left(-\dfrac{1}{3}\right).60^2=600\left(m\right)\)

Vậy quãng đường đoàn tàu đi được từ lúc hãm phanh đến khi dừng hẳn là \(600\left(m\right)\)

help

help

Tổng quãng đường người đó đi \(A\rightarrow B\rightarrow C\rightarrow B:\)

\(S=AB+BC+BC=500+600+600=1700\left(m\right)\)

Độ dịch chuyển của người này trong cả chuyến là :

\(\overrightarrow{S'}=\overrightarrow{AB}+\overrightarrow{BC}-\overrightarrow{BC}=\overrightarrow{AB}\)

\(\Rightarrow\left|\overrightarrow{S'}\right|=\left|\overrightarrow{AB}\right|=500\left(m\right)\)

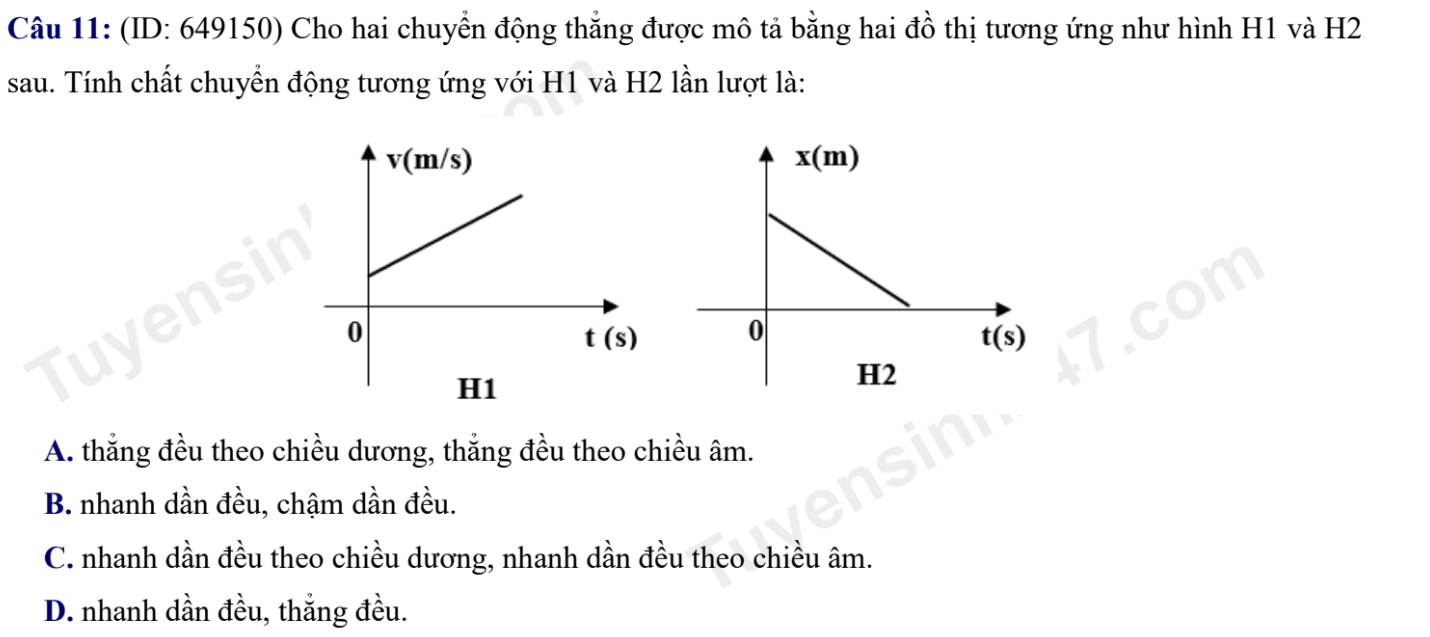
Đồ thị H1 là đồ thị vận tốc- thời gian có đồ thị dốc lên nên là nhanh dần đều

Còn đồ thị H2 là đồ thị độ dịch chuyển- thời gian có đồ thị dốc xuống nên là thẳng đều

Nên D là đúng

\(H1\left(v;t\right):\) có phương trình chuyển động là \(v=v_o+at\) là chuyển động nhanh dần đều vì \(a=tan\alpha>0\) (đường xiên lên so với phương ngang quay 1 góc \(\alpha\) theo chiều kim đồng hồ)

\(H2\left(x;t\right):\) có phương trình chuyển động là \(x=x_o+vt\) đồ thị có đường đi xuống thẳng đi xuống \(\left(v=tan\alpha< 0\right)\) nên vật sẽ chuyển động thẳng đều nhưng ngược hướng với chiều chuyển động

\(\Rightarrow\) Chọn D

\(v_o=64,8\left(km/h\right)=18\left(m/s\right)\)

\(v=50,4\left(km/h\right)=14\left(m/s\right)\)

a) \(v^2-v_o^2=2as\Rightarrow a=\dfrac{v^2-v_o^2}{2s}=\dfrac{14^2-18^2}{2.40}=-1,6\left(m/s^2\right)\)

\(\Rightarrow\) Đúng

b) Khi dừng hẳn \(\Rightarrow v_t=0\)

\(v_t=v_o+at\Rightarrow t=\dfrac{v_t-v_o}{a}=\dfrac{0-18}{-1,6}=11,25\left(s\right)\)

\(\Rightarrow\) Sai

c) Quãng đường tổng cộng ô tô đi được đến khi dừng hẳn:

\(v_t^2-v_o^2=2as\Rightarrow s=\dfrac{v_t^2-v_o^2}{2a}=\dfrac{0^2-18^2}{2.\left(-1,6\right)}=101,25\left(m\right)< 102\left(m\right)\)

\(\Rightarrow\)  xe dừng lại trước khi chạm vào chướng ngại vật \(\Rightarrow\) Đúng

d) \(v_{tb}=\dfrac{101,25}{11,25}=9\left(m/s\right)\)

\(\Rightarrow\) Đúng

a) Đúng

b) \(v_{13}=35\left(km/h\right);v_{23}=27\left(km/h\right)\)

\(v_{12}=v_{13}-v_{23}=35-27=8\left(km/h\right)\)

\(\Rightarrow\) Đúng

c) \(s_1=35t;s_2=20+27t\)

Để 2 xe gặp nhau \(s_1=s_2\Leftrightarrow35t=20+27t\Leftrightarrow8t=20\Leftrightarrow t=2,5\left(h\right)\)

\(\Rightarrow\) Đúng

d) \(s_A=s_1=35t=35.2.5=87,5\left(km\right)\)

\(s_B=s_2=20+27t=20+27.2,5=87,5\left(km\right)\)

\(\Rightarrow\) Đúng

a) Chọn gốc tọa độ tại \(A\), chiều dương \(A\rightarrow B\), gốc thời gian là lúc 2 xe ô tô cùng xuất phát

Phương trình quãng đường của xe ô tô xuất phát từ \(A:s_1=40t\left(km\right)\)

Phương trình quãng đường của xe ô tô xuất phát từ \(B:s_2=20+30t\left(km\right)\)

- Với \(t=1,5\left(h\right)\Rightarrow\left\{{}\begin{matrix}s_1=40.1,5=60\left(km\right)\\s_2=20+30.1,5=65\left(km\right)\end{matrix}\right.\)

Khoảng cách giữa 2 xe \(\left|s_2-s_1\right|=\left|65-60\right|=5\left(km\right)\)

\(\Rightarrow\) Xe ô tô tại \(A\) cách xe ô tô tại \(B\) 1 đoạn \(5\left(km\right)\)

- Với \(t=3\left(h\right)\Rightarrow\left\{{}\begin{matrix}s_1=40.3=120\left(km\right)\\s_2=20+30.3=110\left(km\right)\end{matrix}\right.\)

Khoảng cách giữa 2 xe \(\left|s_2-s_1\right|=\left|110-120\right|=10\left(km\right)\)

\(\Rightarrow\) Xe ô tô tại \(A\) đã vượt xe ô tô tại \(B\) 1 đoạn \(10\left(km\right)\)

b) Để 2 xe gặp nhau khi :

\(s_1=s_2\)

\(\Rightarrow40t=20+30t\)

\(\Rightarrow10t=20\)

\(\Rightarrow t=2\left(h\right)\)

\(\Rightarrow\) Vị trí 2 xe gặp nhau cách \(A\) một đoạn \(s_1=40.2=80\left(km\right)\)

Bài 3 : Chọn trục tọa độ \(xOy\), với \(Ox//\overrightarrow{v_o}\); \(Oy//\overrightarrow{P}\), gốc thời gian là từ lúc bắt đầu ném đá.

a) Phương trình chuyển động \(\left\{{}\begin{matrix}x=v_ot=18t\\y=\dfrac{gt^2}{2}=4,9t^2\end{matrix}\right.\)

b) Phương trình quỹ đạo của hòn đá :

\(y=\dfrac{g}{2v_o^2}x^2=\dfrac{9,8}{2.18^2}x^2=\dfrac{4,9}{324}x^2\)

\(\Rightarrow\) Quỹ đạo của hòn đá là một đường cong parabol

c) Thời gia hòn đá chạm mặt nước \(h=50\left(m\right)\)

\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.50}{9,8}}=3,2\left(s\right)\)

d) Tốc độ của hòn đá lúc chạm mặt nước là hợp của vận tốc theo trục \(Ox\) và \(Oy\) tại thời điểm đó.

Vận tốc theo phương ngang \(Ox\) không đổi: \(v_x=v_o=18\left(m/s\right)\)

Vận tốc theo phương dọc \(Oy\) tại thời điểm \(t=3,2\left(s\right):\)

\(v_y=gt=9,8.3,2=31,4\left(m/s\right)\)

Tốc độ tổng hợp lúc chạm mặt nước:

\(v=\sqrt{v_x^2+v_y^2}=\sqrt{18^2+\left(31,4\right)^2}=36,2\left(m/s\right)\)

Theo quy tắc tổng hợp lực 2 vec tơ đồng quy ta có :

\(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\)

\(\Rightarrow F^2=F_1^2+F_2^2+2F_1F_2cos\alpha\)

\(\Rightarrow cos\alpha=\dfrac{F^2-\left(F_1^2+F_2^2\right)}{2F_1F_2}=\dfrac{7,8^2-\left(4^2+5^2\right)}{2.4.5}=0,496\)

\(\Rightarrow\alpha=60,3^o\)