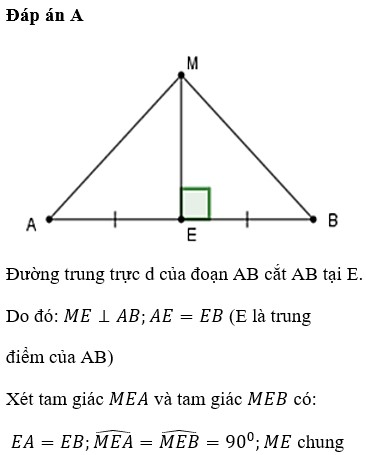
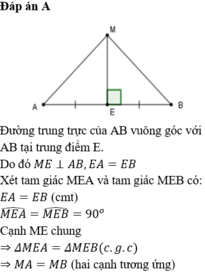
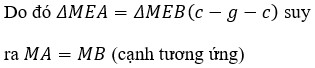Cho đoạn thẳng AB, trên đường trung trực d của đoạn thẳng AB lấy điểm M . Chứng minh AM = BM .

Những câu hỏi liên quan
Cho đoạn thẳng AB, trên đường trung trực d của đoạn thẳng AB lấy điểm M. So sánh AM với BM?
A. MA=MB
B. MA>MB
C. MB=A<MB
D. 2MA=MB
Cho đoạn thẳng AB, trên đường trung trực d của đoạn AB lấy điểm M. So sánh AM và BM
A. MA=MB
B. MA>MB
C. MA<MB
D. 2MA=MB
Cho đoạn thẳng AB.Đường trung trực của đoạn thẳng AB cắt AB tại I. Lấy điểm M bất kì nằm trên đường trung trực của đoạn thẳng AB.
a/ Chứng minh: AM=MB.
b/ Chứng minh: MI là tia phân giác của góc AMB.
c/ Biết : Góc AMB bằng \(^{ }\)\(110^o\) . Hãy tính số đo góc ngoài tại đỉnh A.
a: Ta có: M nằm trên đường trung trực của AB
nên MA=MB
b: Ta có: ΔMAB cân tại M
mà MI là đường trung trực
nên MI là đường phân giác
Đúng 1
Bình luận (1)
cho tam giác abc vuông tại a có AB =6cm BC=10CM
a trên tia đối của tia AB lấy điểm D sao cho AD =AB gọi K là trung điểm của cạnh BC , ĐƯỜNG thẳng DK cắt tại AC tại M chứng minh BC = CD và tính độ dài đoạn thẳng AM
B ĐƯỜNG trung trực d của đoạn thẳng AC CẮT ĐƯỜNG thẳng DC tại Q CHỨNG Minh 3 điểm B,M,Q thẳng hàng
a: AC=8cm
Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
hay CB=CD
Xét ΔCBD có
DK là đường trung tuyến
CA là đường trung tuyến
DK cắt CA tại M
Do đó: M là trọng tâm
=>AM=AC/2=8/3(cm)
b: Xét ΔCAD có
G là trung điểm của AC
GQ//AD
Do đó: Q là trung điểm của CD
Vì M là trọng tâm của ΔCDB nên B,M,Q thẳng hàng
Đúng 4
Bình luận (0)
\(Cho góc xOy, có Ot là tia phân giác. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Vẽ đoạn thẳng AB cắt Ot tại M. Chứng minh a) OAM = OBM; b) AM = BM; OM AB c) OM là đường trung trực của AB d) Trên tia Ot lấy điểm N . Chứng minh NA = NB \)
Cho đường tròn (O), dây AB cố định không đi qua O; Lấy hai điểm C và D thuộc
dây AB sao cho AC = CD = DB. Các bán kính qua C và D cắt cung nhỏ AB tại E và
F.
a) Chứng minh AE < EF
b) Một điểm M di động trên đường tròn (O), điểm P thuộc đoạn thẳng AM, điểm Q
thuộc đoạn thẳng BM sao cho AP = BQ. Chứng minh đường trung trực của PQ luôn
đi qua điểm cố định.
Cho tam giác ABC có AB bé hơn AC, AM là tia phân giác của góc A ( M thuộc BC ). Trên tia AC lấy điểm D sao cho AD=AB
a) Chứng minh BM=MD
b) Gọi K là giao điểm của AB và DM. Chứng minh tam giác tam giác DAK=tam giác BAC
c) Chứng minh AM là đường trung trực của đoạn thẳng BD
Cho tam giác ABC nhọn AB< AC vẽ AD là phân giác của góc BAC D thuộc BC trên cạnh lấy điểm M sao cho AM = AB
a) Chứng minh tam giác ABD bằng tam giác ABD
b) Chứng minh tam giác BDM cân tại D
c) chứng chứng minh AD là đường trung trực của đoạn thẳng BM
a: Sửa đề: Chứng minh ΔABD=ΔAMD
Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: DB=DM
=>D nằm trên đường trung trực của BM(1)
ta có: AB=AM
=>A nằm trên đường trung trực của BM(2)
Từ (1),(2) suy ra AD là đường trung trực của BM
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn AB< AC vẽ AD là phân giác của góc BAC D thuộc BC trên cạnh lấy điểm M sao cho AM = AB
a) Chứng minh tam giác ABD bằng tam giác AMD
b) Chứng minh tam giác BDM cân tại D
c) chứng chứng minh AD là đường trung trực của đoạn thẳng BM
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM
Đúng 0
Bình luận (0)