cho hình vuông ABCD có cạnh bằng a. Gọi E;F;G;H lần lượt là trung điểm các cạnh AB;BC;CD;DA. M là giao điểm của CE và DF
a.CMR tam giác MAD cân
b. Tính \(S_{MDC}\)theo a
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a√2; SA vuông góc (ABCD) và SA=2a . Gọi E là hình chiếu vuông góc của A trên cạnh SB .
4.1. Chứng minh BD ⊥ (SAC) .
4.2. Chứng minh BC ⊥ (SAB) và (AEC) ⊥ (SBC) .
4.3. Gọi G và K lần lượt là trọng tâm của các tam giác SAD và ACD Tính góc giữa đường thẳng GK và mặt phẳng (SAB) .
Tham khảo nhé!
https://hoc24.vn/cau-hoi/cho-hinh-chop-sabc-co-tam-giac-abc-vuong-tai-a-goc-abc60-sbaba-hai-mat-ben-sab-va-sbc-cung-vuong-goc-voi-mat-day-goi-hk-lan-luot-la.898787451803
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA = a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE
A. 14 πa 2
B. 11 πa 2
C. 8 πa 2
D. 12 πa 2
Đáp án A
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
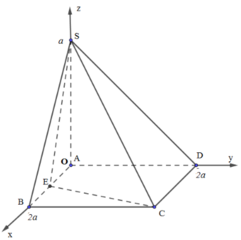
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
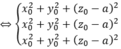
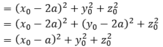
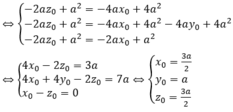
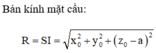
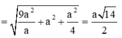
![]()
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông góc với mặt phẳng đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích của khối chóp S. ABCD bằng a 3 3 . Tính khoảng cách từ A đến mặt phẳng (SBE).
A. 2 a 3
B. a 2 3
C. a 3
D. a 3 3
cho hình vuông abcd có cạnh bằng a. N là điểm tùy ý thuộc cạnh AB. Gọi E là giao điểm của CN và DA
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy ABCD. Góc giữa SC và mặt đáy bằng 45 ° . Gọi E là trung điểm BC. Tính khoảng cách giữa hai đường thẳng DE và SC
A. a 38 19
B. a 5 5
C. a 38 5
D. a 5 19
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA=a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
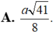

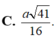
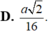
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA=a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
A. a 41 8 .
B. a 41 24 .
C. a 41 16 .
Đáp án A
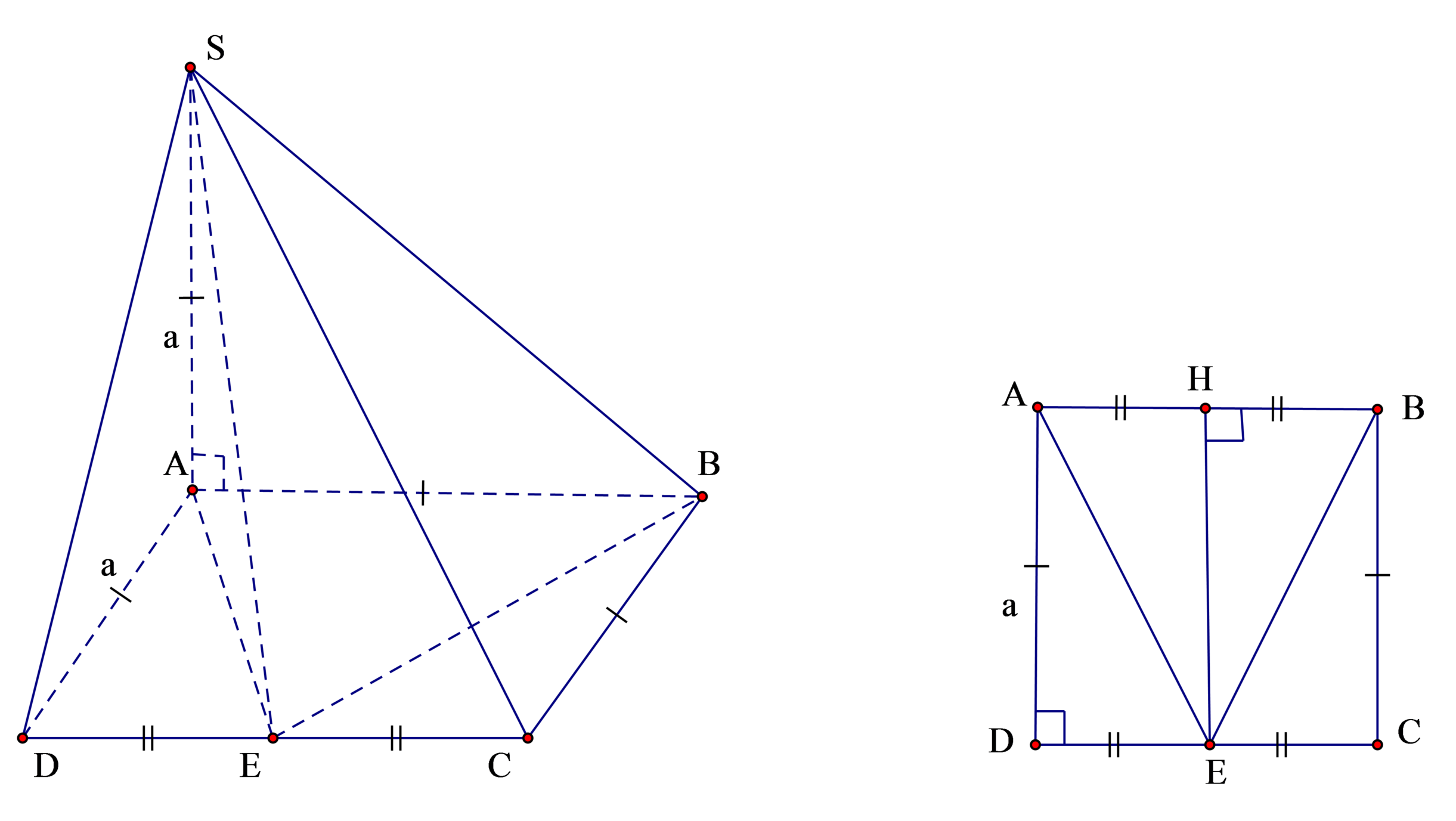
Hình chóp SABE có cạnh bên S A ⊥ đáy (ABE) ta có công thức tính bán kính mặt cầu của hình chóp dạng này là R = R d 2 + h 2 2 ( với R d là bán kính đường tròn ngoại tiếp đáy và h là chiều cao hình chóp )
Ta có: h = S A = a ; d t A B E = 1 2 E H . A B = a 2 2
A E = B E = a 2 + a 2 4 = a 5 2
R d = A B . A E . B E 4 d t A B E = a . 5 a 2 4 4. a 2 2 = a 5 8
vậy R = 25 a 64 2 + a 2 4 = a 41 8 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA=a Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
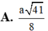
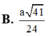
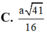
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA = a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
A. a 41 8
B. a 41 24
C. a 41 16
D. a 2 16
Đáp án A
Tam giác ABE cân có A E = B E = a 5 2
và AB = a
⇒ S Δ A B E = a 2 2 = A E . B E . A B 4. R Δ A B E ⇒ R Δ A B E = 2 a . a 5 2 2 : 4 a 2 = 5 a 8
Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABE là
R = R Δ A B E 2 + S A 2 4 = 5 a 8 2 + a 2 4 = a 41 8
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, sạnh bên SA vuông góc với mặt đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích khối chóp S.ABCD bằng a 3 3 . Khoảng cách từ điểm A đến mặt phẳng (SBE) bằng