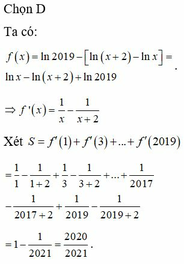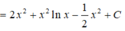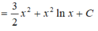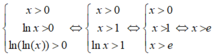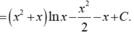tính nguyên hàm (lnx -1)/(x^2-ln^2x)
Những câu hỏi liên quan
Cho hàm số
f
x
ln
2019
-
ln
x
+
2
x
. Tính tổng
S
f
1
+
f
3
+
...
Đọc tiếp
Cho hàm số f x = ln 2019 - ln x + 2 x . Tính tổng S = f ' 1 + f ' 3 + . . . + f ' 2019 .
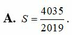
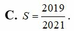
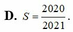
Tính nguyên hàm \(\int\dfrac{lnx}{x\left(2ln^2x-1\right)^3}dx\)
\(\int\dfrac{lnx}{x\left(2ln^2x-1\right)^3}dx\)
\(t=2ln^2x-1\Rightarrow dt=\dfrac{4}{x}lnxdx\Rightarrow dx=\dfrac{x.dt}{4lnx}\)
\(\Rightarrow\int\dfrac{lnx}{x\left(2ln^2x-1\right)^3}dx=\int\dfrac{lnx}{x\left(2ln^2x-1\right)^3}.\dfrac{xdt}{4lnx}=\dfrac{1}{4}\int\dfrac{dt}{t^3}=\dfrac{1}{4}.\left(-\dfrac{1}{2}\right).t^{-2}=-\dfrac{1}{8\sqrt{2ln^2x-1}}\)
Đúng 2
Bình luận (0)
Họ các nguyên hàm của hàm số f(x)(2x+1)lnx là A.
x
2
+
x
ln
x
-
x
2
2
+
x
+
C
B.
x
2...
Đọc tiếp
Họ các nguyên hàm của hàm số f(x)=(2x+1)lnx là
A. x 2 + x ln x - x 2 2 + x + C
B. x 2 + x ln x - x 2 2 - x + C
C. x 2 + 1 ln x - x 2 2 - x + C
D. 2 ln x + 1 2 + C
22 tháng 4 2022 lúc 0:06
Tính nguyên hàm I = \(\int\left(x^2+2x\right)ln\left(3x+1\right)dx\)
Họ nguyên hàm của hàm số f(x) 2x ( 2 + ln x) là A. . B. . C. . D. .
Đọc tiếp
Họ nguyên hàm của hàm số f(x) = 2x ( 2 + ln x) là
A. 
.
B. 
.
C. 
.
D. 
.
Tìm miền xác định của hàm số y = ln(ln(lnx))
A. D = (0; +∞)
B. D = (1; +∞)
C. D = (e; +∞)
D. D = ( e e ; + ∞ )
Họ các nguyên hàm của hàm số f(x) (2x + 1) ln x là A. . B. . C. . D. .
Đọc tiếp
Họ các nguyên hàm của hàm số f(x) = (2x + 1) ln x là
A. 
.
B. 
.
C. 
.
D. 
.
Cho bốn hàm số sau : y f(x) lnx ;
y
g
(
x
)
2
x
2
+
4
;
y
h
(
x
)
2017
1018
x
và y l(x) ln( x2+1). Có bao nhiêu hàm số...
Đọc tiếp
Cho bốn hàm số sau : y= f(x) = lnx ; y = g ( x ) = 2 x 2 + 4 ; y = h ( x ) = 2017 1018 x và
y= l(x)= ln( x2+1). Có bao nhiêu hàm số đồng biến trên khoảng ( 0 ; + ∞ )
A. 1
B. 2
C. 3
D. 4
+ Sử dụng tính chất: Hàm số y= logax đồng biến trên TXĐ khi a> 1nên y= f(x) = lnx
là hàm số đồng biến.
+ Sử dụng tính chất: Hàm số y= ax nghịch biến trên R khi 0< a< 1nên
Chọn C
Đúng 0
Bình luận (0)
18 tháng 11 2023 lúc 21:06
4. Tính đạo hàm của các hàm số sau:
a) \(y = (3x^2-4x+1)^{-4}\)
b) \(y = 3^{x^2-1} + e^{-x+1}\)
c) \(y = \ln (x^2-4x) + \log_{3} (2x-1)\)
d) \(y =x . \ln x + 2^{\frac{x-1}{x+1}}\)
e) \(y = x^{-7} - \ln (x^2-1)\)
`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
Đúng 3
Bình luận (0)
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)
Đúng 3
Bình luận (0)