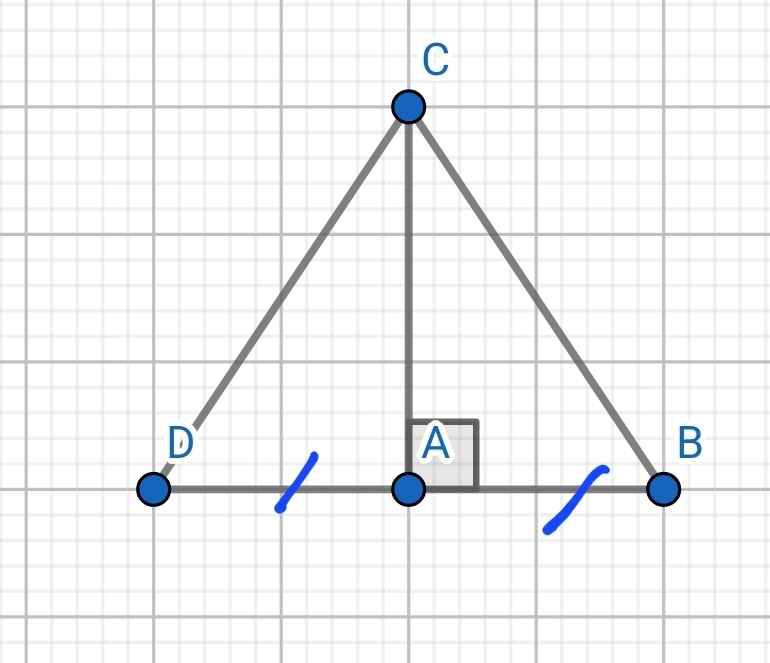
a) Xét hai tam giác vuông: ∆ABC và ∆ADC có:

AC chung

AB = AD (gt)

⇒ ∆ABC = ∆ADC (hai cạnh góc vuông)

b) Do ∆ABC = ∆ADC (cmt)

⇒ ∠BCA = ∠DCA (hai góc tương ứng)

⇒ CA là tia phân giác của ∠BCD

a: Xét ΔABC vuông tại A có 

\(BC^2=AB^2+AC^2\)

nên BC=50(cm)

Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(AB^2=BH\cdot BC\)

hay BH=18(cm)

Ta có: ΔBAC vuông tại A

mà AM là đường trung tuyến ứng với cạnh huyền BC

nên \(MB=MC=\dfrac{BC}{2}=25\left(cm\right)\)

Bạn có thể viết lại đề bài cho rõ hơn được không ạ?

b)   Chứng minh tg ABC đồng dạng với tg DBA
c) CM AB^2=BC.BD

a, Theo pytago \(BC^2-AB^2+AC^2\)

                        \(\Rightarrow BC^2=6^2+8^2=100\)

                        \(\Rightarrow BC=10cm\)

Ta có: \(AD.10=6.8\)

        \(\Rightarrow AD=4,8cm\)

b, Xét \(\Delta ABC\) và \(\Delta DBA\) có:

\(\widehat{A}=\widehat{D}\)(=90 độ)

\(\widehat{C}\)chung

\(\Rightarrow\Delta ABC\sim\Delta DBA\)

c, Vì \(\Delta ABC\sim\Delta DBA\)

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BD}{BA}\)

\(\Rightarrow AB^2=BC.BD\)

-chúc bạn học tốt-

Bài 1: 

a: Ta có ΔABC cân tại A
mà AD là đường phân giác ứng với cạnh đáy BC

nên AD⊥BC

b: Ta có: AE+BE=AB

AF+FC=AC

mà BE=CF

và AB=AC

nên AE=AF

Xét ΔAED và ΔAFD có 

AE=AF

\(\widehat{EAD}=\widehat{FAD}\)

AD chung

Do đó: ΔAED=ΔAFD

Suy ra: \(\widehat{EDA}=\widehat{FDA}\)

hay DA là tia phân giác của \(\widehat{EDF}\)

1:

BC=15+20=35cm

AD là phân gíac

=>AB/BD=AC/CD

=>AB/3=AC/4=k

=>AB=3k; AC=4k

AB^2+AC^2=BC^2

=>25k^2=35^2

=>k=7

=>AB=21cm; AC=28cm

AH=21*28/35=16,8cm

\(AD=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)

2:

BC=căn 12^2+16^2=20cm

HB=AB^2/BC=12^2/20=7,2cm

HC=20-7,2=12,8cm

a: d//AD

AD cắt AC tại A

Do đó: d cắt AC tại E

b: Gọi Ax là tia đối của tia AB

=>góc xAC là góc ngoài tại đỉnh A của ΔABC

=>AD là phân giác của góc xAC

AD//BE

=>góc xAD=góc ABE và góc DAE=góc AEB

mà góc xAD=góc DAE

nên góc ABE=góc AEB

c: b vuông góc AD

d//AD

Do đó: b vuông góc d

Em tự vẽ hình nhé

a) Xét \(\Delta BED\) và \(\Delta CFD\) có: 

\(\widehat{BED}=\widehat{CFD}=90^0\);

\(\widehat{BDE}=\widehat{CDF}\) (đối đỉnh)

\(\Rightarrow\Delta BED\sim\Delta CFD\) (g.g)

b) Xét \(\Delta ABE\) và \(\Delta ACF\) có:

\(\widehat{AEB}=\widehat{AFC\:}=90^0\);

\(\widehat{BAE}=\widehat{CAF}\) (tính chất phân giác)

\(\Rightarrow\Delta ABE\sim\Delta ACF\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AF}\Rightarrow AB.AF=AC.AE\)

c) Do \(BE//FC\) (cùng vuông góc \(AD\))

\(\Rightarrow\dfrac{SB}{SF}=\dfrac{BE}{FC}\) mà \(\dfrac{BE}{FC}=\dfrac{BD}{CD}\) (do \(\Delta BED\sim\Delta CFD\))

Lại có \(\dfrac{BD}{CD}=\dfrac{AB}{AC}\) (tính chất tia phân giác); \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\) (câu b)

\(\Rightarrow\dfrac{SB}{SF}=\dfrac{AE}{AF}\Rightarrow SA//BE\) (ĐL Ta-let đảo)

\(\Rightarrow SA//CF\Rightarrow SA\perp AF\)

bạn cần bài nào

2 BÀI CHẢ BT HỎI BÀI NÀO

Cần bài nào hả bn