Tam giác ABC cân tại A (BC<AB). Trên cạnh AB lấy điểm D sao cho CD=CB
a) C/m góc ACB= góc CDB
b) Trên tia đối của tia CA lấy E sao cho CE=AD
C/m BE=BA
Bài 1: Cho tam giác ABC cân tại A. Lấy D, E thuộc BC sao cho BD = CF. CMR: tam giác ABC cân tại A.
Bài 2: Tam giác ABC cân tại A. Lấy M thuộc AB, N thuộc AC sao cho AM = AN.
a) CMR: MN//BC.
b) Cho CM cắt BN tại I. CMR: IB = IC.
Bài 3: Tam giác ABC cân tại A. Lấy M thuộc BC. Vẽ MK//AB (K thuộc AC). CMR: MK = KC.
Cho tam giác ABC cân tại C khi đó
Cho Tam giác ABC cân tại C khi đó
A. AB = AC.
B. AC = BC
C. BC = BA.
D. AB = AC = BC
Cho tam giác ABC có BC=a. Dựng ra ngoài ABC các tam giác ABE vuông cân tại B và tam giác ACF vuông cân tại C.Gọi M là trung điểm EF. Kẻ MH vuông góc với BC tại H. Tính MH theo a |
Cho tam giác ABC cân tại A có A ^ = 100 o ,BC=a,AC=b. Về phía ngoài tam giác ABC vẽ tam giác ABD cân tại D có A D B ^ = 140 o . Tính chu vi tam giác ABD theo a và b
A. 2a + b
B. a - b
C. 2a - b
D. 2a - 2b
cho tam giác abc cân tại a vẽ tam giác abd và tam giác ace vuông cân tại a
chứng minh de//bc
Cho tam giác ABC có 2 góc B và C nhọn. Vẽ phíc ngoài tam giác ABC các tam giác vuông cân ABD (cân tại B) và tam giác ACE (cân tại C). Vẽ DI và IK vuông góc với BC(I,K thuộc BC). CMR:
a) BI = CK
b) BC = ID + EK
Cho tam giác ABC cân tại A có góc A = 100 độ, BC=a, AC= b.Vẽ về phía ngoài tam giác ABC tam giác ABD cân tại D có góc ADB= 140 độ. Tính chu vi tam giác ABD
Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E. Chứng minh rằng AECB là hình thang vuông
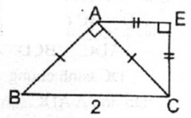
Tam giác ABC vuông cân tại A
⇒ ∠ (ACB) = 45 0
Tam giác EAC vuông cân tại E
⇒ ∠ (EAC) = 45 0
Suy ra: ∠ (ACB) = ∠ (EAC)
⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
nên tứ giác AECB là hình thang có ∠ E = 90 0 . Vậy AECB là hình thang vuông
Cho tam giác ABC cân tại A, tia phân giác góc A cắt BC tại D.
a) Chứng minh DB = DC.
b) Kẻ DH AB (HAB), DK AC (KAC). Chứng minh DHK cân.
c) Chứng minh HK // BC. Cho tam giác ABC cân tại A, tia phân giác góc A cắt BC tại D.
a) Có \(\Delta\)ABC cân tại A (gt), AD là phân giác \(\widehat{BAC}\)(D\(\in\)BC)
=> AD là đường phân giác của \(\Delta\)ABC
Mà trong tam giác cân đường phân giác trùng với đường trung tuyến
=> D là trung điểm của BC
=> DB=DC (đpcm)
b) Xét hai tam giác vuông ΔAKD và ΔAKD
Ta có: AD cạnh chung
\(\widehat{CAD}=\widehat{BAD}\left(gt\right)\)
\(\widehat{AHD}=\widehat{AKD}=90^o\)
Vậy ΔAKD=ΔAKD(cạnh huyền.góc nhọn)
Vậy DK=DH (cạnh tương ứng)
Nên ΔDHK cân
c. Do ΔAHK có AK=AH nên cân
Vậy \(\widehat{AKH}=\widehat{AHK}=\frac{180^o-\widehat{KAH}}{2}\)
Do ΔABC cân nên \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{KAH}}{2}\)
Nên \(\widehat{AKH}=\widehat{ACB}\) mà hai góc trên ở vị trí đồng vị nên HK//BC
Cho tam giác ABC cân tại a có B=100°. BC=a; AC=b. Về phía ngoài tam giác ABC vẽ tan giác ABD cân tại D có ADB=140°. Tính chu vi tam giác theo a và b