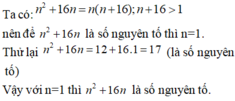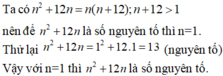Ta có:\(P=n^3-n^2+7n+10\)

\(=n^3-2n^2+n^2-2n-5n+10\)

\(=n^2\left(n-2\right)+n\left(n-2\right)-5\left(n-2\right)\)

\(=\left(n-2\right)\left(n^2+n-5\right)\)

Vì P là số nguyên tố nên 

\(n-2=1\Rightarrow n=3\)(nhận)

\(n^2+n-5=1\)\(\Rightarrow n^2+n-6=0\Rightarrow\left(n+3\right)\left(n-2\right)=0\Rightarrow n=-3\left(l\right);n=2\left(n\right)\)

Ta có:\(\hept{\begin{cases}n=3\Rightarrow P=7\left(n\right)\\n=2\Rightarrow P=0\left(l\right)\end{cases}}\)

Vậy n=3

\(P=n^3-n^2-7n+10=\left(n-2\right)\left(n^2+n-5\right)\)

- Với \(n-2< 0\Leftrightarrow n< 2\).

Bằng cách thử trực tiếp \(n=0,n=1\)thu được \(n=1\)thỏa mãn \(P=3\)là số nguyên tố. 

- Với \(n-2\ge0\)thì \(n-2\ge0,n^2+n-5>0\)khi đó \(P\)có hai ước tự nhiên là \(n-2,n^2+n-5\).

Để \(P\)là số nguyên tố thì: 

\(\orbr{\begin{cases}n-2=1\\n^2+n-5=1\end{cases}}\Leftrightarrow\orbr{\begin{cases}n=3\\n=2,n=-3\end{cases}}\)

Thử lại các giá trị trên thu được \(n=3\)thì \(P=7\)thỏa mãn. 

Vậy \(n=1\)hoặc \(n=3\). 

`P=n^3-n^2+n-1`

`=n^2(n-1)+(n-1)`

`=(n-1)(n^2+1)`

Vì n là stn thì p là snt khi

`n-1=1=>n=2`

Vậy n=2

Đáp án cần chọn là: C

Đáp án cần chọn là: D

Xét 2 trường hợp:

TH1: n = 0

5ⁿ + 10 = 5⁰ + 10 = 11 là số nguyên tố

TH2: n ≠ 0

Ta có:

5ⁿ ⋮ 5

10 ⋮ 5

⇒ (5ⁿ + 10) ⋮ 5

⇒ 5ⁿ + 10 là hợp số

Vậy n = 0 thì 5ⁿ + 10 là số nguyên tố

Nếu đề bài là:

   5ⁿ⁺¹⁰ \(\in\) P 

⇔ 5ⁿ⁺¹⁰ = 5

⇒ n + 10 = 1

⇒ n = -9 (loại)

n \(\in\) \(\varnothing\)

Nếu đề bài là:

    5ⁿ + 10 \(\in\) P

   với n = 0 ta có 5ⁿ + 10 = 11 (thỏa mãn)

   Với n ≥ 1 ta có 5ⁿ + 10 = \(\overline{..5}\) + 10 = \(\overline{...5}\) (là hợp số loại)

Vậy n = 0

TH1. Đề bài là: 5ⁿ + 10 \(\in\) P

               Với n = 0 ⇒ 5ⁿ + 10 = 1 + 10 = 11 (thỏa mãn)

               Với n ≥ 1 ⇒ 5ⁿ + 10 = \(\overline{..5}\)+ 10 = \(\overline{..5}\) ⋮ 5 (loại)

 Vậy n = 0

TH2. Đề bài là: 5^{n +10} \(\in\) P 

           5ⁿ⁺¹⁰ \(\in\) P ⇔ n + 10 = 1 

           ⇒ n = -9 (loại)

   n \(\in\) \(\varnothing\)

\(P=\dfrac{n^3+3n^2+2n}{6}+\dfrac{2n+1}{1-2n}\)

Vì n^3+3n^2+2n=n(n+1)(n+2) là tích của 3 số liên tiếp

nên n^3+3n^2+2n chia hết cho 3!=6

=>Để P nguyên thì 2n+1/1-2n nguyên

=>2n+1 chia hết cho 1-2n

=>2n+1 chia hết cho 2n-1

=>2n-1+2 chia hết cho 2n-1

=>\(2n-1\in\left\{1;-1;2;-2\right\}\)

=>\(n\in\left\{1;0;\dfrac{3}{2};-\dfrac{1}{2}\right\}\)