Số 2^29 là một số tự nhiên có 9 chữ số khác nhau.Hãy chỉ ra một chữ số không có mặt trong số đó?
Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là:
A . 504 59049
B . 7560 59049
C . 1260 59049
D . 12600 59049
Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: ![]()
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: ![]()
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: 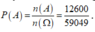
Từ tập hợp tất cả các số tự nhiên có 5 chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Tính xác suất để trong số tự nhiên lấy ra được chỉ có mặt 3 chữ số khác nhau.
Câu 33. Từ tập hợp X = \{1; 2; 3; 4; 5; 6; 7; 8; 9\} ta thành lập được các số tự nhiên có 6 chữ s hat 0 . lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau.
Có bao nhiêu số tự nhiên có 9 chữ số đôi một khác nhau sao cho có mặt đồng thời bốn chữ số 4;5;6;7và bốn chữ số đó đôi một không kề nhau?
Có bao nhiêu số tự nhiên có 9 chữ số đôi một khác nhau sao cho có mặt đồng thời bốn chữ số 4;5;6;7 và bốn chữ số đó đôi một không kề nhau?
Chọn 5 chữ số còn lại từ 6 chữ số 0,1,2,3,8,9 có \(C_6^5\) cách
Xếp thứ tự 5 chữ số ở trên: \(5!\) cách
5 chữ số trên tạo thành 6 khe trống, xếp 4 chữ số 4,5,6,7 vào 6 khe trống đó: \(A_6^4\) cách
\(\Rightarrow C_6^5.5!.C_6^4\) số (bao gồm cả trường hợp số 0 đứng đầu)
Chọn 5 chữ số sao cho có mặt chữ số 0: \(C_5^4\) cách
Xếp 5 chữ số đó sao cho số 0 đứng đầu: 4! cách (hoán vị 4 chữ số còn lại)
4 chữ số tạo thành 5 khe trống, xếp 4,5,6,7 vào 5 khe trống: \(A_5^4\) cách
Vậy số số thỏa mãn là: \(C_6^5.5!.A_6^4-C_5^4.4!.A_5^4\) số
Bạn An nghĩ ra một số tự nhiên có tính chất kì lạ : khi nhân số đó với 7 được tích là số chỉ chứa một chữ số lập lại nhiều lần và chữ số lập lại đó khác chữ số 7. Bạn có biết bạn An nghĩ ra số nào không, biết rằng số đó là số tự nhiên nhỏ nhất thỏa mãn tính chất trên
Đáp án
Theo đề bài, tích của số đó với 7 là: aa...a = a x 11...1 (với a khác 7, a khác 0 vì nếu a = 0 thì tích là số 0, không phải là số có 1 chữ số lặp lại). Số này chia hết cho 7 mà a là chữ số từ 1 đến 9 và khác chữ số 7 nên 11...1 phải chia hết cho 7. Số tự nhiên nhỏ nhất thì a = 1 và số 11...1 nhỏ nhất.
Ta xét các số có chữ số 1 lặp lại từ bé đến lớn để tìm ra số bé nhất chia hết cho 7. Ta có:
11 không chia hết cho 7
111 không chia hết cho 7
1 111 không chia hết cho 7
11 111 không chia hết cho 7
111 111 chia hết cho 7
Vậy tích kết quả nhỏ nhất là số 111 111 và số tự nhiên cần tìm là: 111 111 : 7 = 15873
bạn An nghĩ ra một số tự nhiên có tính chất kì lạ: khi nhân số đó với 7 thì được tích là số chỉ chứa một chữ lặp lại nhiều lần và chữ số lặp lại đó khác chữ số 7. Bạn có biết An nghĩ ra số nào không? Biết rằng số đó là số đó là số tự nhiên nhỏ nhất thỏa mãn tính chất trên.
Bạn An nghĩ ra một số tự nhiên có tính chất kỳ lạ: khi nhân số đó với 7 thì được tích là số chỉ chứa một chữ số lặp lại nhiều lần và chữ số lặp lại đó khác chữ số 7 (tức là tích kết quả có dạng aa...a , với a khác 7). Bạn có biết số An nghĩ ra là số nào không? Biết rằng số đó là số tự nhiên nhỏ nhất thỏa mãn tính chất trên.
Bạn An nghĩ ra một số tự nhiên có tính chất kỳ lạ: khi nhân số đó với 7 thì được tích là số chỉ chứa một chữ số lặp lại nhiều lần và chữ số lặp lại đó khác chữ số 7 (tức là tích kết quả có dạng aa...a , với a khác 7). Bạn có biết số An nghĩ ra là số nào không? Biết rằng số đó là số tự nhiên nhỏ nhất thỏa mãn tính chất trên