Tính giá trị của 2ab2, biết a = 4, b = 6

Những câu hỏi liên quan
Tính tích tất cả các giá trị thực của tham số m để đồ thị hàm số y =m x3- 3mx2+ 3m-3 có hai điểm cực trị A; B sao cho 2AB2- ( OA2+ OB2) =20 .
A. 1
B. ½
C. -17/11
D. 13/ 5
Ta có: đạo hàm y’ = m( 3x2-6x). Để hàm số đã cho có 2 điểm cực trị thì m≠ 0.
Với mọi m≠ 0 , ta có
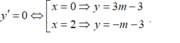
Gọi tọa độ 2 điểm cực trị là A( 0 ; 3m-3) và B( 2 ; -m-3)
Ta có :
2 A B 2 - ( O A 2 + O B 2 ) = 20 ⇔ 11 m 2 + 6 m - 17 = 0 ⇔ m = 1
hoặc m = - 17 11
Vậy giá trị m cần tìm là:

Chọn C.
Đúng 0
Bình luận (0)
ính giá trị của biểu thức
1/ (-25). ( -3). x với x = 4
2/ (-1). (-4) . 5 . 8 . y với y = 25
3/ (2ab2) : c với a = 4; b = -6; c = 12
4/ [(-25).(-27).(-x)] : y với x = 4; y = -9
giúp mk với ^^^
1/ (-25). ( -3). x với x = 4
= ( -25 ) . ( -3 ) . 4
= [ -25 . 4 ] . ( -3 )
= -100 . ( -3 )
= 300
2/ (-1). (-4) . 5 . 8 . y với y = 25
= ( -1 ) . ( -4 ) . 5 . 8 . 25
= [ -1 . 5 . 8 ] . [ -4 . 25 ]
= -40 . ( -100 )
= 4000
4/ [(-25).(-27).(-x)] : y với x = 4; y = -9
= [ -25 . ( -27 ) . ( -4 ) ] . ( -9 )
= -25 . ( -27 ) . ( -4 ) . ( -9 )
= [ -25 . ( -4 ) ] . [ -27 . ( -9 ) ]
= 100 . 243
= 2430
Đúng 2
Bình luận (0)
1/(-25).(-3).4 x=4
=75.4
=300
2/(-1).(-4).5.8.y y=25
=(-1).(-4).5.8.25
=4.40.25
=(4.25).40
=100.40
4000
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
m
x
3
-
3
m
x
2
+
3
m
-
3
có hai điểm cực trị A,B sao cho
2
A...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = m x 3 - 3 m x 2 + 3 m - 3 có hai điểm cực trị A,B sao cho 2 A B 2 - ( O A 2 + O B 2 ) = 20 ( Trong đó O là gốc tọa độ).
A. m = -1
B. m = 1
C. m = - 1 h o ặ c m = - 17 11 .
D. m = 1 h o ặ c m = - 17 11 .
Chọn D
Ta có: y ' = m ( 3 x 2 - 6 x )
Với mọi m ≠ 0, ta có y ' = 0
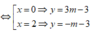 .
.
Vậy hàm số luôn có hai điểm cực trị.
Giả sử A ( 0 ; 3 m - 3 ) ; B ( 2 ; - m - 3 ) .
Ta có
![]()
![]()
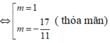
Vậy giá trị m cần tìm là:
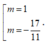
Đúng 0
Bình luận (0)
Cho các biểu thức sau
A = \(\dfrac{4}{x+2}+\dfrac{2}{x-2}+\dfrac{5x-6}{4-x^2}\)
B = \(\dfrac{x+1}{x^2+3x+2}\)
a. Rút gọn A, B
b. tính giá trị của A biết x2 + x = 0
Tính giá trị của B biết x2 + 2x = 0
\(a,ĐK:x\ne\pm2\\ A=\dfrac{4x-8+2x+4-5x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x-2}\\ ĐK:x\ne-1;x\ne-2\\ B=\dfrac{x+1}{\left(x+1\right)\left(x+2\right)}=\dfrac{1}{x+2}\\ b,x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\\ \forall x=0\Leftrightarrow A=\dfrac{1}{0-2}=-\dfrac{1}{2}\\ \forall x=-1\Leftrightarrow A=\dfrac{1}{-1-2}=-\dfrac{1}{3}\)
\(x^2+2x=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-2\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=0\\ \Leftrightarrow B=\dfrac{1}{0+2}=\dfrac{1}{2}\)
Đúng 6
Bình luận (0)
Giả sử x và y là 2 đại lượng tỉ lệ thuận . x1, x2 là hai giá trị khác nhau của x. y1, y2 là hai giá trị tương ứng của y.
a) Tính x1 biết x2= -2, y1= 4 ,y2= 6
b) Tính x1, y1 biết y1 - x1 = -2, x2= -3, y2=6
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
Câu 5:
\(D\left(2\right)=21a+9b-6a-4b\)
\(D\left(2\right)=\left(21a-6a\right)+\left(9b-4b\right)\)
\(D\left(2\right)=15a+5b\)
Mà: \(3a+b=18\Rightarrow b=18-3b\)
\(\Rightarrow D\left(2\right)=15a+5\left(18-3b\right)\)
\(D\left(2\right)=15a+90-15a\)
\(D\left(2\right)=90\)
Vậy: ...
Đúng 2
Bình luận (3)
Câu 4:
\(D\left(1\right)=4a+10b-b+2a\)
\(D\left(1\right)=\left(4a+2a\right)+\left(10b-b\right)\)
\(D\left(1\right)=6a+9b\)
Mà: \(2a+3b=12\Rightarrow a=\dfrac{12-3b}{2}\)
\(\Rightarrow D\left(1\right)=6\left(\dfrac{12-3b}{2}\right)+9b\)
\(D\left(1\right)=\dfrac{6\left(12-3b\right)}{2}+9b\)
\(D\left(1\right)=3\left(12-3b\right)+9b\)
\(D\left(1\right)=36-9b+9b\)
\(D\left(1\right)=36\)
Vậy: ...
Đúng 2
Bình luận (0)
Câu 3:
Sửa đề: \(C=5a-4b+7a-8b\)
\(C=\left(5a+7a\right)-\left(4b+8b\right)\)
\(C=12a-12b\)
\(C=12\left(a-b\right)\)
\(C=12\cdot8\)
\(C=96\)
Vậy: ...
Đúng 2
Bình luận (0)
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
4:
D=6a+9b=3(2a+3b)=36
5:
D=15a+5b=5(3a+b)=90
Đúng 0
Bình luận (0)
Câu 3: Tính giá trị của biểu thức C 5a − 4b + 7a + 8 . Biết a-b8.
Câu 4: Tính giá trị của biểu thức D 4a + 10b - b+ 2a. Biết 2a+3b12
Câu 5: Tính giá trị của biểu thức D21a + 9b — 6a — 4b. Biết 3a+b18
Đọc tiếp
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
Câu 5:
D=21a+9b-6a-4b
=21a-6a+9b-4b
=15a+5b
=5(3a+b)
\(=5\cdot18=90\)
Câu 4: D=4a+10b-b+2a
=4a+2a+10b-b
=6a+9b
=3(2a+3b)
\(=3\cdot12=36\)
Câu 3:
C=5a-4b+7a+8
=5a+7a-4b+8
=12a-12b+8b+8
=12(a-b)+8b+8
=8(a-b)+8b+8
=8a-8b+8b+8
=8a+8
Đúng 0
Bình luận (0)
Bài 1) Tính giá trị của M
M= 3 x 4 x 5 + 4 x 5 x 6 + ... + 13 x 14 x 15
Bài 2) Tính giá trị của A, biết rằng
M= 1/1x4 + 1/4x7 + 1/7x10+ ...+ 1/97x100
Bài 1:
$M=3.4.5+4.5.6+...+13.14.15$
$4M=3.4.5(6-2)+4.5.6(7-3)+....+13.14.15(16-12)$
$=-2.3.4.5+3.4.5.6-3.4.5.6+4.5.6.7+....-12.13.14.15+13.14.15.16$
$=-2.3.4.5+13.14.15.16=43560$
$M=43560:4=10890$
Đúng 1
Bình luận (0)
Bài 2:
a.
$3M=\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.10}+...+\frac{3}{97.100}$
$=\frac{4-1}{1.4}+\frac{7-4}{4.7}+\frac{10-7}{7.10}+...+\frac{100-97}{97.100}$
$=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{97}-\frac{1}{100}$
$=1-\frac{1}{100}=\frac{99}{100}$
$M=\frac{99}{100}:3=\frac{33}{100}$
Đúng 1
Bình luận (0)

















