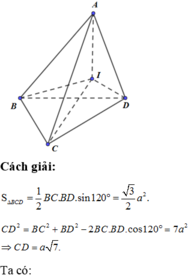
Cho tứ giác ABCD có AC+AD=<BC+BD. CMR: AD<BD

Những câu hỏi liên quan
Cho tứ giác ABCD có AB = CB, AD = AC = CD và góc A = 105 độ. Tính các góc của tứ giác ABCD.
Cho tứ giác ABCD có AB+BD bé hơn hoặc bằng AC+CD. CMR AD<AC
Cho tứ giác ABCD có AD = DC, đường chéo AC là phân giác góc Â. Chứng minh rằng ABCD là hình thang.
Xét ΔADC có DA=DC
nên ΔADC cân tại D
Suy ra: \(\widehat{DAC}=\widehat{DCA}\)
mà \(\widehat{DAC}=\widehat{BAC}\)
nên \(\widehat{BAC}=\widehat{ADC}\)
hay AB//CD
Xét tứ giác ABCD có AB//CD
nên ABCD là hình thang
Đúng 0
Bình luận (0)
Câu 17:. Chọn câu đúng:A. Tứ giác ABCD là hình chữ nhật khi có và . B. Tứ giác ABCD là hình chữ nhật khi có và . C. Tứ giác ABCD là hình chữ nhật khi có ABCD; ADBC; ACBD. D. Tứ giác ABCD là hình chữ nhật khi có ABCD; ABBC và ACBD.
Đọc tiếp
Câu 17:. Chọn câu đúng:
A. Tứ giác ABCD là hình chữ nhật khi có và
.
B. Tứ giác ABCD là hình chữ nhật khi có và
.
C. Tứ giác ABCD là hình chữ nhật khi có AB=CD; AD=BC; AC=BD.
D. Tứ giác ABCD là hình chữ nhật khi có AB=CD; AB=BC và AC=BD.
Cho tứ giác ABCD có góc A=Góc D, BC=AD và DB là phân giác góc D. Chứng minh :
a) tứ giác ABCD là hình thang vuông
b) AC^2+AD^2=DC^2+BD^2
cho tứ giác ABCD có AD=BC. Gọi M, N, P, Q lần lượt là trung AB, AC, CD, BD
a/Tứ giác ABCD là hình Gì
b/Tứ giác ABCD cần có thêm điều kiện gì để MNPQ là hình chữ nhật
a) Ta có : \(AD=BC\left(gt\right)\)
=> ABCD là hình thang cân ( 2 cạnh bên = nhau )
b) Để MNPQ là hình chữ nhật thì \(\widehat{P}_1=90^o\)
Vì ABCD là hình thang cân ( câu a )
\(\Rightarrow AB//CD\)
Gọi I , K là 2 điểm nối từ A , B đến cạnh CD và vuông góc với CD
\(\Rightarrow AI//BK\) ( cùng vuông góc với CD )
Ta lại có : \(\widehat{P}_1=\widehat{K}\)( đ.vị ) (1)
Mà \(\widehat{K}=90^o\left(gt\right)\) (2)
Từ (1) và (2) \(\Rightarrow MNPQ\)là hình chữ nhật ( có góc = 90 độ )
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AD = AB, AC = BD. Chứng minh ABCD là hình thang cân.
Cho tứ diện ABCD có ABACAD2a. Biết tam giác BCD có BC2a, BDa,
C
B
D
^
120
°
. Tính thể tích tứ diện ABCD theo a
Đọc tiếp
Cho tứ diện ABCD có AB=AC=AD=2a. Biết tam giác BCD có BC=2a, BD=a, C B D ^ = 120 ° . Tính thể tích tứ diện ABCD theo a
![]()
![]()
![]()
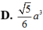
Cho tứ diện ABCD có AB AC AD 2a. Biết tam giác BCD có BC 2a, BD a,
C
B
D
^
120
0
. Tính thể tích tứ diện ABCD theo a. A.
5
3
a
3
B.
5
2
a
3...
Đọc tiếp
Cho tứ diện ABCD có AB = AC = AD = 2a. Biết tam giác BCD có BC = 2a, BD = a, C B D ^ = 120 0 . Tính thể tích tứ diện ABCD theo a.
A. 5 3 a 3
B. 5 2 a 3
C. 5 a 3
D. 5 6 a 3
Phương pháp:
Sử dụng các công thức diện tích tam giác ![]() và công thức Cosin
và công thức Cosin ![]()
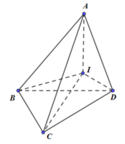
Cách giải:
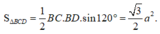
![]()
![]()
Ta có: ![]()
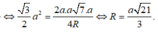
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD.
Do AB = AC = AD ![]()
![]()
Thể tích tứ diện ABCD là 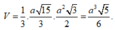
Chọn D.
Đúng 0
Bình luận (0)