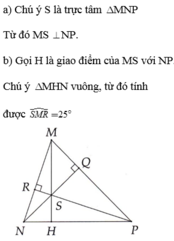
Cho tam giác MNP có ba góc nhọn, các đường cao NQ,PR cắt nhau tại S . Chứng minh MS vuông với NP .

Những câu hỏi liên quan
Cho tam giác MNP có ba góc nhọn, các đường cao NQ, PR cắt nhau tại S.
a) Chứng minh M S ⊥ N P .
b) Cho M N P ^ = 45 ° . Tính S M R ^ .
Cho tam giác MNP có 3 góc nhọn , các đường cao NQ , PR cắt nhau tại S
a) Chứng minh MS vuông góc NP
b) Cho góc MNP = 65°. Tính góc SMR
a) Xét ΔMNP có
NQ là đường cao ứng với cạnh MP
PR là đường cao ứng với cạnh MN
MP cắt MN tại S
Do đó: MS\(\perp\)NP
b) Ta có: MS\(\perp NP\)(cmt)
nên \(\widehat{SMN}+\widehat{MNP}=90^0\)
hay \(\widehat{SMN}=25^0\)
Đúng 2
Bình luận (0)
Cho \(\Delta\)MNP có 3 góc nhọn,các đường cao NQ,PR cắt nhau tại S
a)Chứng minh MS\(\perp\)NP
b)Cho góc MNP=65 độ tính góc SMR
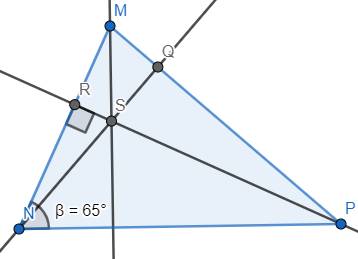
a) Theo đề ta có S là trực tâm của tam giác MNP và MNP là tam giác nhọn
Suy ra MS cũng là đường cao đáy NP, hay \(MS\perp NP\)
b) Gọi O là giao điểm của MS và NP. Ta có MNO là tam giác vuông tại O
Suy ra \(\widehat{MNO}+\widehat{NMO}=90^o\) hay \(\widehat{MNP}+\widehat{SMR}=90^o\)
Suy ra \(\widehat{SMR}=90^o-\widehat{MNP}=90^o-65^o=25^o\)
Đúng 0
Bình luận (0)
Cho tam giác MNP có 3 góc nhọn,các đường cao NQ,PR cắt nhau tại S.
a)Cm MS vuông góc với NP
b)cho ^MNP=65*.tính SMR^
a/ Xét t/g MNP có 2 đg cao NQ ; PR cắt nhautaij S
=> S là trực tâm t/g MNP
=> MS vg góc NP
b/ Có MS vuông góc NP
=> \(\widehat{MNP}+\widehat{SMR}=90^o\)
\(\Rightarrow\widehat{SMR}=25^o\)
Đúng 1
Bình luận (0)
Cho tam giác nhọn MNP .Các đường cao PB,NA cắt nhau tại H a,c/m tam giác MBP đồng dạng với tan giác MAN;từ đó suy ra MB=MA.MP b,MH cắt NP tại C.C/m MC vuông góc với NP c,C/m NB.NM+PA.MP=NP Hộ mình bài này với
a) Xét ΔMBP vuông tại B và ΔMAN vuông tại A có
\(\widehat{BMP}\) chung
Do đó: ΔMBP\(\sim\)ΔMAN(g-g)
Suy ra: \(\dfrac{MB}{MA}=\dfrac{MP}{MN}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MB\cdot MN=MA\cdot MP\)
Đúng 0
Bình luận (0)
b) Xét ΔMNP có
NA là đường cao ứng với cạnh MP(gt)
PB là đường cao ứng với cạnh MN(gt)
NA cắt PB tại H(gt)
Do đó: H là trực tâm của ΔMNP(Tính chất ba đường cao của tam giác)
Suy ra: MH\(\perp\)NP tại C
Đúng 1
Bình luận (0)
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H chứng minh:
A, tam giác ABE vuông góc với tâm giác ACF
B, AEF = ABC
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\hat{EAB}\) chung
Do đo: ΔAEB~ΔAFC
b: ΔAEB~ΔAFC
=>\(\frac{AE}{AF}=\frac{AB}{AC}\)
=>\(\frac{AE}{AB}=\frac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\frac{AE}{AB}=\frac{AF}{AC}\)
góc FAE chung
Do đó: ΔAEF~ΔABC
=>\(\hat{AEF}=\hat{ABC}\)
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M có MN=5cm, MP=12cm và đường cao MH.
a. Chứng minh: tam giác MNP đồng dạng tam giác HNM. Từ đó suy ra MN^2=NH.NP
b. Tính NP,NH.
c. Cho NQ là phân giác của góc MNP (Q thuộc MP). Chứng minh: QM/QP và QM,QP.
d. Gọi E là giao điểm MH và NQ. Tính tỉ số S^MNQ/S^HNE
a: Xét ΔMNP vuông tại M và ΔHNM vuông tại H có
góc N chung
DO đó: ΔMNP∼ΔHNM
Suy ra: NM/NH=NP/NM
hay \(NM^2=NH\cdot NP\)
b: NP=13cm
\(NH=\dfrac{MN^2}{NP}=\dfrac{25}{13}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC . M là điểm nằm trong tam giác . Các tia AM,BM,CM cắt BC, CA,AB tại N,P,Q. Qua M kẻ đường song song với BC cắt NP , NQ tại E và F. Chứng minh :
a. ME=MF
b. Giả sử AM vuông góc với BC. Chứng minh góc MNP= góc MNQ
cho tam giác MNP nhọn có K là trung điểm của NP đường thẳng vuông góc với KM tại N cắt đường thẳng MK tại E trên tia KM láy H sao cho KH=KE
chứng minh PH vuông MN
Sửa đề: PH vuông góc với MH
Xét tứ giác NEPH có
K là trung điểm của đường chéo EH
K là trung điểm của đường chéo NP
Do đó: NEPH là hình bình hành
Suy ra: NE//HP
mà NE⊥MH
nên HP⊥HP
Đúng 1
Bình luận (0)