Cho tam giác ABC vuông tại A, góc B=60 độ. Gọi M là trung điểm của cạnh BC, trên tia đối của tia AM lấy điểm D sao cho AM=MD
a) Chứng minh rằng: tam giác ABC= tam giác DCB
b) Chứng minh rằng: tam giác ABD là tam giác vuông
c) Tính số đo góc BMD
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A,M là trung điểm của.Trên tia đối của tia MA lấy điểm D sao cho MA=MD
A) Chứng minh rằng:Tam giác AMC =Tam giác DMB
B) Chứng minh rằng: Tam giác ABD vuông
C) So sánh : AM và BC
a: Xét ΔAMC và ΔDMB có
MC=MB
\(\widehat{AMC}=\widehat{DMB}\)
MA=MD
DO đó: ΔAMC=ΔDMB
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: ΔABD vuông
c: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=BC/2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông góc tại A trên cạnh BC lấy điểm E sao cho BE=BA. Tia phjan6 giác của góc B cắt AC tại D
a/ Chứng minh tam giác ABD =tam giác EBD
b/ DE vuông góc BC
c/ trên tia đối của tia AC lấy điểm M sao cho AM=AB trên cạnh AB lấy điểm N sao cho AN = AD. Chứng minh tam giác ABD=tam giác AMN
d/ gọi H là trung điểm MN , K là trung điểm BD . Chứng minh góc HAK = 90 độ
Bài 1. Cho tam giác ABC vuông tại A có góc B 53 độa) Tính góc C.b) Trên cạnh BC, lấy một điểm D sao cho BDBA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh tam giác BEA tam giác BED.Bài 2. Cho tam giác ABC có AB AC và M là trung điểm của cạnh BC.a) Chứng minh tam giác AMB tam giác AMC.b) Qua A, vẽ đường thẳng a vuông góc với AM. Chứng minh AM vuông góc với BC và a song song với BC.c) Qua C, vẽ đường thẳng b song song với AM. Gọi N là giao điểm của hai đường thẳng a và b. Chứng minh...
Đọc tiếp
Bài 1. Cho tam giác ABC vuông tại A có góc B= 53 độ
a) Tính góc C.
b) Trên cạnh BC, lấy một điểm D sao cho BD=BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh tam giác BEA = tam giác BED.
Bài 2. Cho tam giác ABC có AB= AC và M là trung điểm của cạnh BC.
a) Chứng minh tam giác AMB = tam giác AMC.
b) Qua A, vẽ đường thẳng a vuông góc với AM. Chứng minh AM vuông góc với BC và a song song với BC.
c) Qua C, vẽ đường thẳng b song song với AM. Gọi N là giao điểm của hai đường thẳng a và b. Chứng minh tam giác AMC = tam giác CNA.
Bài 3. Cho tam giác ABC, gọi M là trung điểm của cạnh BC. Trên tia đối của tia MAlấy điểm D sao cho MD = MA.
a) Chứng minh tam giác MAB = tam giác MDC.
b) Chứng minh rằng AB = CD và AB // CD.
Bài 4. Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE = BA. Vẽ AH vuông góc với BC tại H.
a) Chứng minh rằng: tam giác ABD = tam giác EBD và AD = ED.
b) Chứng minh rằng: AH // DE.
*Vẽ hình giúp mình*
bài 1
có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0=>\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-90^0-53^0=37^0\)
b) xét 2 tam giác của đề bài có
góc ABE = góc DBE
BD=BA
BE chung
=> 2 tam giác = nhau
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC . Phân giác của góc ABC cắt AC tại I. Biết BỊ vuông góc với AM tại H. a Chứng minh rằng 1A IM . b Tính các góc của tam giác BIC . c Biết độ dài các cạnh của tam giác ABC là ba số nguyên dương liên tiếp đơn vị centimet , tính chu vi của tam giác ABC theo centimet . d Trên tia đối của tia HB lấy điểm K sao cho HK HB . Chứng minh rằng AAIB AKIC .
a. Xét tam giác BID và tam giác CID có :
AI=ID ( giả thiết )
BI=CI ( vì I là trung điểm của BC )
góc BID=góc CIA ( đối đỉnh )
Nên tam giác BID= tam giác CIA ( c- g- c)
Cho tam giác ABC có ABAC, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy E sao cho AD AEa. Chứng minh rằng tâm giác AMB tam giác AMCb. Chứng minh rằng AM là tia phân giác của góc A và AM vuông góc với BCc. Gọi K là giao điểm của AM và DE. Chưng minh AK vuông góc với DEd. trên tia đối của tia ED lấy đeiểm F sao cho FE MC, gọi H là trung điểm của EC. Chứng minh 3 điểm M, H, F thẳng hàng
Đọc tiếp
Cho tam giác ABC có AB=AC, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy E sao cho AD= AE
a. Chứng minh rằng tâm giác AMB = tam giác AMC
b. Chứng minh rằng AM là tia phân giác của góc A và AM vuông góc với BC
c. Gọi K là giao điểm của AM và DE. Chưng minh AK vuông góc với DE
d. trên tia đối của tia ED lấy đeiểm F sao cho FE= MC, gọi H là trung điểm của EC. Chứng minh 3 điểm M, H, F thẳng hàng
HOI KHO ^.^
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM CNa) Chứng minh rằng tam giác AMN là tam giác cânb) Kẻ BH vuông góc với AM ( H thuộc AM ). Kẻ CK vuông góc với AN ( K thuộc AN ). Chứng minh rằng BH CKc) Chứng minh rằng AH AKd) Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác gì? Vì sao?e) Khi góc MAN 60 độ và BM CN BC, hãy tính số đo các góc của tam giác ABC
Đọc tiếp
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BH vuông góc với AM ( H thuộc AM ). Kẻ CK vuông góc với AN ( K thuộc AN ). Chứng minh rằng BH = CK
c) Chứng minh rằng AH = AK
d) Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác gì? Vì sao?
e) Khi góc MAN = 60 độ và BM = CN = BC, hãy tính số đo các góc của tam giác ABC
14 tháng 12 2023 lúc 23:35
cho tam giác ABC vuông tại A có góc B bằng 60 độ. Gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho DM=MA
a)Tính góc ACB
b)Chứng minh: Tam giác ABM=tam giác DCM và AB//CD
c)Chứng minh: AM=1/2 BC
cho tam giác ABC vuông tại A. gọi M là trung điểm của BC. trên tia đối của tia MA lấy điểm E sao cho ME= MA. Chứng Minh rằng rằng:
a, tam giác AMB = tam giác EMC
b, AC vuông góc với CE
c, BC = 2.AM
Lời giải:
a.
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Lấy M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh rằng a) tam giác ABC= tam giác CDA b) AM=½BC
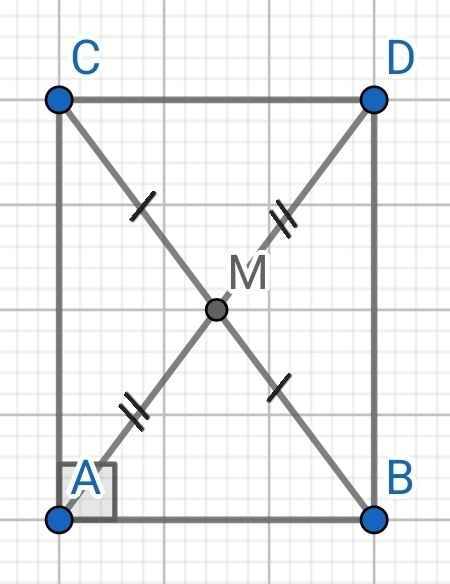
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆AMB và ∆DMC có:
AM = DM (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆AMB = ∆DMC (c-g-c)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
Lại có:
∠MAC + ∠MAB = 90⁰ (∆ABC vuông tại A)
⇒ ∠MAC + ∠MDC = 90⁰
⇒ ∠DAC + ∠ADC = 90⁰
∆CDA có:
∠DAC + ∠CDA + ∠ACD = 180⁰ (tổng ba góc trong ∆ACD)
⇒ ∠ACD = 180⁰ - (∠DAC + ∠CDA)
= 180⁰ - 90⁰
= 90⁰
⇒ ∆ACD vuông tại C
Do ∆AMB = ∆DMC (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABC và ∆CDA có:
AC là cạnh chung
AB = CD (cmt)
⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)
b) Do ∆ABC = ∆CDA (cmt)
⇒ BC = AD (hai cạnh tương ứng)
Do AM = DM (gt)
⇒ AM = DM = ½AD
Mà AD = BC (cmt)
⇒ AM = ½BC
Đúng 1
Bình luận (0)
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
DO đó: ABDC là hình bình hành
Suy ra: AB=DC; AC=BD
Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=1/2BC
Đúng 2
Bình luận (0)