 Giúp mình với mình cảm ơn mọi người rất nhiều 🥰
Giúp mình với mình cảm ơn mọi người rất nhiều 🥰

Những câu hỏi liên quan
Mình đang cần gấp😱, nhờ mọi người giúp mình với ạ. Cảm ơn mọi người nhiều!!!🥰🥰🥰


Mn ơi giúp mình vs được ko ạ mình phải nộp gấp r !!! Cảm ơn mn rất nhiều 🥰🥰🥰
Mình sẽ tặng coin cho người làm đầu tiên nha
Đúng 0
Bình luận (0)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)
Đúng 1
Bình luận (0)
d: Xét ΔCBD có
CA là đường cao ứng với cạnh DB
BK là đường cao ứng với cạnh CD
CA cắt BK tại F
Do đó: F là trực tâm của ΔCBD(Tính chất ba đường cao của tam giác)
Suy ra: DF\(\perp\)BC
Ta có: DF\(\perp\)BC(cmt)
AH\(\perp\)BC(gt)
Do đó: DF//AH(Định lí 1 từ vuông góc tới song song)
Xét ΔFAB vuông tại A và ΔFAD vuông tại A có
FA chung
AB=AD
Do đó: ΔFAB=ΔFAD
Suy ra: FB=FD(hai cạnh tương ứng
Xét ΔFBD có FB=FD
nên ΔFBD cân tại F
e: Xét ΔFBD có
A là trung điểm của BD
AE//DF
Do đó: E là trung điểm của BF
Đúng 0
Bình luận (0)
Mọi người ơi giúp mình với mình đang cần gấp mình cảm ơn mọi người rất nhiều

mọi người giúp mình với ạ , mình cảm ơn rất nhiều
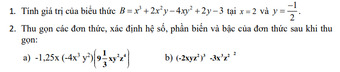
mọi người giúp mình với ạ , mình cảm ơn rất nhiều !!!!!!!
Bài 1 :
Thay x = 2 ; y = -1/2 ta được
\(B=-8+2.4\left(-\dfrac{1}{2}\right)-4.2.\left(\dfrac{1}{4}\right)+2\left(-\dfrac{1}{2}\right)-3\)
\(=-8-4-2-1-3=-18\)
Đúng 2
Bình luận (0)
Giúp mình với ạ. Mình cảm ơn mọi người rất nhiều!!!

a) Ta có: \(\left(2x-3\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\3x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{3}{2};-\dfrac{4}{3}\right\}\)
b) Ta có: \(x^3-3x^2+3x-1=\left(x-1\right)\left(x+1\right)\)
\(\Leftrightarrow\left(x-1\right)^3-\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2-2x+1-x-1\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-3x\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=3\end{matrix}\right.\)
Vậy: S={0;1;3}
c) Ta có: \(x^2+x=2x+2\)
\(\Leftrightarrow x\left(x+1\right)-2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
Vậy: S={-1;2}
d) Ta có: \(\left(x-1\right)^2=2\left(x^2-1\right)\)
\(\Leftrightarrow\left(x-1\right)^2-2\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-1-2x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)Vậy: S={1;-3}
e) Ta có: \(2\left(x+2\right)^2-x^3-8=0\)
\(\Leftrightarrow2\left(x+2\right)^2-\left(x^3+8\right)=0\)
\(\Leftrightarrow2\left(x+2\right)\cdot\left(x+2\right)-\left(x+2\right)\left(x^2-2x+4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x+4-x^2+2x-4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\cdot\left(-x^2+4x\right)=0\)
\(\Leftrightarrow-x\left(x+2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=4\end{matrix}\right.\)
Vậy: S={0;-2;4}
Đúng 1
Bình luận (0)

mọi người giúp mình với ạ mình cảm ơn rất nhiều
a: \(P=-\left|5-x\right|+2019\le2019\forall x\)
Dấu '=' xảy ra khi x=5
Đúng 1
Bình luận (0)
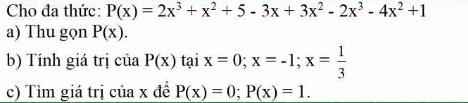
mọi người giúp mình với ạ,mình cảm ơn rất nhiều
a: P(x)=2x^3-2x^3+x^2+3x^2-4x^2-3x+5x+1=-3x+6
b: P(0)=-3*0+6=6
P(-1)=6+3=9
P(1/3)=-1+6=5
c: P(x)=0
=>-3x+6=0
=>-3x=-6
=>x=2
P(x)=1
=>-3x+6=1
=>-3x=-5
=>x=5/3
Đúng 0
Bình luận (0)
 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD⊥BC tại D
Xét tứ giác AHDC có \(\hat{AHC}=\hat{ADC}=90^0\)
nên AHDC là tứ giác nội tiếp
b: AHDC nội tiếp
=>\(\hat{AHD}+\hat{ACD}=180^0\)
mà \(\hat{AHD}+\hat{MHD}=180^0\) (hai góc kề bù)
nên \(\hat{MHD}=\hat{ACD}=\hat{ACB}\)
Xét ΔOAC vuông tại A có AH là đường cao
nên \(OH\cdot OC=OA^2\)
=>\(OH\cdot OC=OB^2\)
=>\(\frac{OH}{OB}=\frac{OB}{OC}\)
Xét ΔOHB và ΔOBC có
\(\frac{OH}{OB}=\frac{OB}{OC}\)
góc HOB chung
Do đó: ΔOHB~ΔOBC
=>\(\hat{OHB}=\hat{OBC}=\hat{ABC}\)
mà \(\hat{OHB}+\hat{MHB}=\hat{OHM}=90^0\) và \(\hat{ABC}+\hat{ACB}=90^0\) (ΔABC vuông tại A)
nên \(\hat{MHB}=\hat{ACB}\)
=>\(\hat{MHB}=\hat{DHM}\)
=>HM là phân giác của góc DHB
Đúng 0
Bình luận (0)
 Mọi người ơi giúp mình với,mình cảm ơn rất nhiều ạ
Mọi người ơi giúp mình với,mình cảm ơn rất nhiều ạ
used to deliver
used to be
used to go
used to drive
used to spend
used to believe
used to work
used to serve
Đúng 2
Bình luận (2)
1. used to deliver
2. used to be
3. used to go
4. used to drive
5. used to spend
6. used to believe
7.used to work
8. used to serve
Đúng 1
Bình luận (0)

















