Cho đường tròn (O) có đường kính BC. Lấy điểm A trên (O) sao cho AC < AB
a) Chứng minh: ABC vuông; tnh độ dài AC và số đo góc ABC biết rằng AB = 8cm và BC = 10cm
b) Tiếp tuyến tại B và tếp tuyến tại A của (O) cắt nhau tại D.
c) Tia DC cắt (O) tại M (M nằm giữa D và C). Gọi H là giao điểm của OD với AB.
Chứng minh: MH ⊥ MA
giải giúp em câu C với ạ

Những câu hỏi liên quan
Cho đường tròn (O; R) có đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O; R), trên đường tròn (O; R) lấy điểm C sao cho .
a/ Chứng minh: Tam giác ABC vuông và tính độ dài AC, BC theo R.
b/ Tia BC cắt Ax tại M, kẻ CH AB tại H. Chứng minh: MC.BC = AH.AB
c/ Gọi I là trung điểm của CH, tia BI cắt AM tại E. Chứng minh: E là trung điểm của AM và EC là tiếp tuyến của đường tròn (O; R).
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
b: Xét ΔABC vuông tại C có CH là đường cao
nên \(AH\cdot AB=AC^2\left(1\right)\)
Xét ΔMAB vuông tại A có AC là đường cao
nên \(MC\cdot BC=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot AB=MC\cdot BC\)
Đúng 0
Bình luận (0)
Cho đường tròn (O;R), kẻ đường kính BC, lấy 1 điểm A trên (O) sao cho AB = R.
a) Chứng minh tam giác ABC vuông. Tính độ dài AC theo R.
b) Trên tia OA lấy D sao cho A là trung điểm của OD. Chứng minh DB là tiếp tuyến của (O).
c) Vẽ tiếp tuyến DM với (O) (M là tiếp điểm). Chứng minh tam giác BDM đều.
mn giúp em với ạ, em cần gấp!
a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó; ΔABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=R\sqrt{3}\)
b: Xét ΔDOB có
BA là đường trung tuyến
BA=DO/2
Do đó: ΔDOB vuông tại B
hay DB là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) và điểm nằm ngoài đường tròn sao cho OA =2R. Vẽ tiếp tuyến AB, trên đường tròn (O) lấy điểm sao cho AB=AC. Chứng minh
a/ AC là tiếp tuyến của đường tròn tâm O
b/ OA vuông BC
c/ Tính AB, AC và bán kính đường tròn ngoại tiếp tam giác ABC theo R
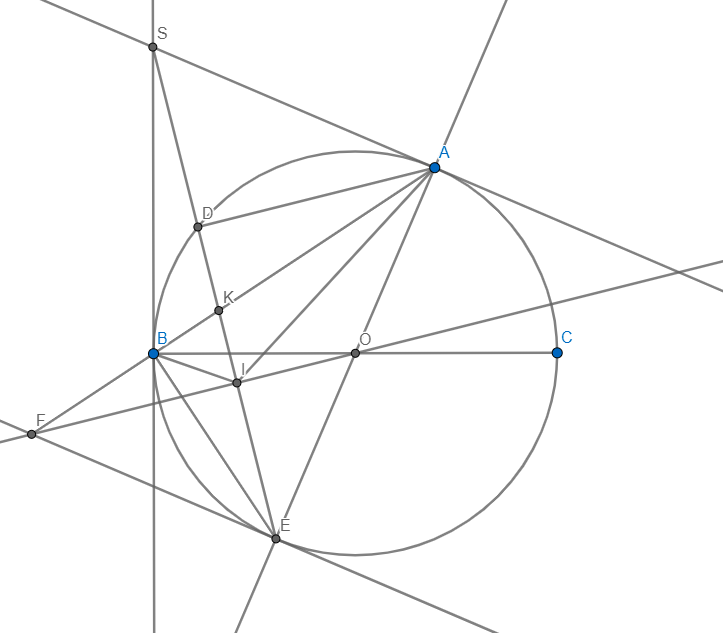
cho đường tròn O có đường kính BC , trên đường tròn O lấy điểm A sao cho ABAC. vẽ các tiếp tuyến tại A và B của đường tròn O cắt nhau tại SA/chứng minh : tứ giác SAOB nội tiếp và SO vuông góc ABB/kẻ đường kính AE của đường trong O ,SE cắt đường trong O tại D. chứng minh SB^2SD.SEC/ gọi I là trung điểm của DE,K là giao điểm của của AB và SE. chứng minh SD.SESK.SID/ vẽ tiếp tuyến tại E của đường tròn O cắt OI tại F .chứng minh 3 điểm A,B,F thẳng hàngthank :33333
Đọc tiếp
cho đường tròn O có đường kính BC , trên đường tròn O lấy điểm A sao cho AB>AC. vẽ các tiếp tuyến tại A và B của đường tròn O cắt nhau tại S
A/chứng minh : tứ giác SAOB nội tiếp và SO vuông góc AB
B/kẻ đường kính AE của đường trong O ,SE cắt đường trong O tại D. chứng minh SB^2=SD.SE
C/ gọi I là trung điểm của DE,K là giao điểm của của AB và SE. chứng minh SD.SE=SK.SI
D/ vẽ tiếp tuyến tại E của đường tròn O cắt OI tại F .chứng minh 3 điểm A,B,F thẳng hàng
thank :33333
a) Ta có: \(\angle SAO+\angle SBO=90+90=180\Rightarrow SAOB\) nội tiếp
Vì SA,SB là tiếp tuyến \(\Rightarrow SA=SB\) và SO là phân giác \(\angle BSA\Rightarrow SO\bot AB\)
b) Xét \(\Delta SBD\) và \(\Delta SEB:\) Ta có: \(\left\{{}\begin{matrix}\angle SBD=\angle SEB\\\angle BSEchung\end{matrix}\right.\)
\(\Rightarrow\Delta SBD\sim\Delta SEB\left(g-g\right)\Rightarrow\dfrac{SB}{SE}=\dfrac{SD}{SB}\Rightarrow SB^2=SD.SE\)
c) Trong (O) có DE là dây cung không đi qua O và I là trung điểm DE
\(\Rightarrow OI\bot DE\Rightarrow\angle OIS=90=\angle OBS\Rightarrow\) OIBS nội tiếp
\(\Rightarrow O,I,B,S,A\) cùng thuộc 1 đường tròn
\(\Rightarrow\) BIAS nội tiếp \(\Rightarrow\angle BIS=\angle BAS=\angle ABS\)
Xét \(\Delta SBK\) và \(\Delta SIB:\) Ta có: \(\left\{{}\begin{matrix}\angle SBK=\angle SIB\\\angle BSIchung\end{matrix}\right.\)
\(\Rightarrow\Delta SBK\sim\Delta SIB\left(g-g\right)\Rightarrow\dfrac{SB}{SI}=\dfrac{SK}{SB}\Rightarrow SB^2=SI.SK\)
mà \(SB^2=SD.SE\Rightarrow SD.SE=SI.SK\)
d) Ta có: \(\angle SIB=\angle SBK=\angle BEA\Rightarrow90-\angle SIB=90-\angle BEA\)
\(\Rightarrow\angle FIB=\angle FEB\Rightarrow FBIE\) nội tiếp
\(\Rightarrow\angle FBE=\angle FIE=90\Rightarrow FB\bot BE\)
mà \(AB\bot BE\left(\angle ABE=90\right)\Rightarrow\) A,B,F thẳng hàng
Đúng 2
Bình luận (3)
Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho H là trung điểm của đoạn thẳng BM. AC cắt đường tròn đường kính CM tại E, EM cắt đường tròn tâm O đường kính BC tại F. Iva A name and mat phon
a) Chứng minh rằng AB // MF.
doi nhau. M và BC
b) Chứng minh rằng tứ giác ABFM là hình thoi. c) Kéo dài AM cắt đường tròn đường kính MC tại I (I +M)
Chứng minh rằng:AI. BO AH.AC
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho H là trung điểm của đoạn thẳng BM. AC cắt đường tròn đường kính CM tại E, EM cắt đường tròn tâm O đường kính BC tại F. Iva A name and mat phon
a) Chứng minh rằng AB // MF.
doi nhau. M và BC
b) Chứng minh rằng tứ giác ABFM là hình thoi. c) Kéo dài AM cắt đường tròn đường kính MC tại I (I +M)
Chứng minh rằng:AI. BO =AH.AC
Cho tam giác ABC (AB<AC) có 3 đỉnh nằm trên đường tròn tâm O. Vẽ đường kính DD' vuông góc với dây BC ( D' thuộc cung ABC). Trên các cạnh AB, AC lấy các điểm M, N sao cho BM = CN.
a, Chứng minh tam giác DMN cân?
b, Đường tròn qua 3 điểm N, A, D' cắt AB kéo dài tại E. Chứng minh BE = BM
Cho đường tròn tâm O có đường kính AB=2R. Trên đường tròn này lấy điếm C sao cho BC=R
a) Vẽ hình trên
b) Chứng minh tam giác ABC vuông
c) tính ABC, tính AC theo R
TA CÓ AB\(=2R\)
\(\Leftrightarrow0B=BC=R\)
HAY \(BC=\frac{1}{2}AB\)
CÓ NGHĨA BC LÀ NỮA TRUNG ĐIỂM CỦA BC
\(\Rightarrow AC\perp BC\)ĐỊNH LÝ 3
Đúng 0
Bình luận (0)
CHO \(R=2cm\)tính cho nó rễ
áp dụng địn lý pi ta gao trong tam giác ABC vuông tại C
\(\Rightarrow AB^2=AC^2+BC^2\)
\(\Rightarrow AC^2=16-4\)
\(\Rightarrow AC=\sqrt{12}cm\)
vậy .............
Đúng 0
Bình luận (0)
cho đường tròn O cò đường kính BC . trên đườn tròn O lấy điểm A sao cho ABAC . vẽ các tiếp tuyến tại A,B của dường tròn O cắt nhau tại SA/ chứng minh tứ giác SAOB nội tiếp và SO vuông góc ABB/ kẻ đường kính AE của đườn tròn O , SE cắt đường tròn O tại D . chứng minh SD^2 SD.SEC/ gọi I là rung điểm của DE , K là giao điểm của AB và SE . chứng minh SD.SESK.SID/ vẽ tiếp tuyến E của đường tròn O cắt tia OI tại F . chứng minh 3 điểm A,B,F thẳng hàngthankkkkkkkkkkkkkkkkkkkkkkkkk
Đọc tiếp
cho đường tròn O cò đường kính BC . trên đườn tròn O lấy điểm A sao cho AB>AC . vẽ các tiếp tuyến tại A,B của dường tròn O cắt nhau tại S
A/ chứng minh tứ giác SAOB nội tiếp và SO vuông góc AB
B/ kẻ đường kính AE của đườn tròn O , SE cắt đường tròn O tại D . chứng minh SD^2 = SD.SE
C/ gọi I là rung điểm của DE , K là giao điểm của AB và SE . chứng minh SD.SE=SK.SI
D/ vẽ tiếp tuyến E của đường tròn O cắt tia OI tại F . chứng minh 3 điểm A,B,F thẳng hàng
thankkkkkkkkkkkkkkkkkkkkkkkkk
a) Xét tứ giác SAOB có
\(\widehat{SAO}+\widehat{SBO}=180^0\left(90^0+90^0=180^0\right)\)
nên SAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét (O) có
SA là tiếp tuyến có A là tiếp điểm(gt)
SB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: SA=SB(Tính chất hai tiếp tuyến cắt nhau)
Ta có: SA=SB(cmt)
nên S nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OA=OB(=R)
nên O nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra SO là đường trung trực của AB
hay SO\(\perp\)AB(Đpcm)
Đúng 2
Bình luận (0)
b) đề phải là \(SA^2=SD.SE\) chứ SD không bằng SE sao \(SD^2=SD.SE\) được
Vì AE là đường kính \(\Rightarrow\angle ADE=90\) mà \(\angle SAE=90\)
\(\Rightarrow\Delta SAE\) vuông tại A có AD là đường cao
\(\Rightarrow SA^2=SD.SE\)
c) Trong (O) có DE là dây cung không đi qua O và I là trung điểm DE
\(\Rightarrow OI\bot DE\Rightarrow\angle OIS=90\Rightarrow\angle OIS=\angle OBS=90\)
\(\Rightarrow OIBS\) nội tiếp mà SAOB nội tiếp (câu a)
\(\Rightarrow O,I,A,S,B\) cùng thuộc 1 đường tròn
\(\Rightarrow AIBS\) nội tiếp \(\Rightarrow\angle AIS=\angle ABS=\angle SAB\) (\(\Delta SAB\) cân tại S)
Xét \(\Delta SAK\) và \(\Delta SIA:\) Ta có: \(\left\{{}\begin{matrix}\angle SIA=\angle SAK\\\angle ISAchung\end{matrix}\right.\)
\(\Rightarrow\Delta SAK\sim\Delta SIA\left(g-g\right)\Rightarrow\dfrac{SA}{SI}=\dfrac{SK}{SA}\Rightarrow SA^2=SK.SI\)
mà \(SA^2=SD.SE\Rightarrow SD.SE=SK.SI\)
d) AB cắt OI tại F'
Vì AE là đường kính \(\Rightarrow\angle ABE=90\Rightarrow F'BE=90\)
\(\Rightarrow\angle F'BE=\angle F'IE\Rightarrow F'BIE\) nội tiếp \(\Rightarrow\angle ABI=\angle F'EI\)
mà \(\angle ABI=\angle ASI\) (AIBS nội tiếp) \(=\angle ASE\)
\(\Rightarrow\angle F'EI+\angle AES=\angle ASE+\angle AES=90\)
\(\Rightarrow\angle F'EO=90\Rightarrow EF'\) là tiếp tuyến \(\Rightarrow\) đpcm
Đúng 1
Bình luận (1)
cho đường tròn tâm O, đường kính BC, lấy điểm a trên cung bc sao cho AB<AC. Trên OC lấy điểm D, từ D kẻ đường thẳng vuông góc với BC cắt AC tại E.
a) chứng minh tứ giác ABDE nội tiếp
b) Chứng minh góc DAE = góc DBE
c) Đường cao AH của tam giác ABC cắt đường tròn tại F. Chứng minh: HF. DC = HC . ED
d) Chứng minh BC là tia phân giác của góc ABF
câu d:
Tam giác BCF nội tiếp (O;BC/2) có cạnh BC là đường kính
=> Tam giác BCF vuông tại F
=>góc BFC=90 độ
Xét 2 tam giác: tam giác CHF và tam giác CFB có:
góc C chung
góc CHF=góc CFB (=90 độ)
Do đó, tam giác CHF đồng dạng với tam giác CFB (g.g)
=> góc CFH=góc CBF (1)
Tứ giác ABFC nội tiếp (O;BC/2)
=> góc CFH=góc ABC (cùng chắn cung AC) (2)
Từ (1) và (2)=> góc CBF=góc ABC (3)
Mà tia BC nằm giữa tia AB và BF (4)
Từ (3) và (4)=> BC là tia phận giác của góc ABF (đpcm)
Đúng 0
Bình luận (0)
Vì DE \(\perp\)BC => \(\widehat{EDB}=90^0\)
\(\widehat{BAC}=90^0\)( góc nội tiếp chắn nửa đường tròn )
Ta có : \(\widehat{EDB}+\widehat{BAE}=90^0+90^0=180^0\)
=> Tứ giác ABDE nội tiếp ( tổng 2 góc đối = 1800 )
Cho đưong tròn tâm O có bán kính R, đường kính AB. Qua điểm A kẻ đường thẳng d vuông góc AB tại A. Trên d lấy điểm C sao cho AC R. Lấy điểm M thuộc dưong tròn (O) sao cho OM vuông góc với CM tại M. a) Chứng minh 4 điểm A, C, O, M thuộc cùng một đường tròn. b) Gọi K là giao điểm thứ 2 của BC với đường tròn (O). Chứng minh: BC BK 4R mũ 2 c) Chứng minh: MB // OC d) Chứng minh: góc CMK gócMBCGIÚP MIK VỚI Ạ
Đọc tiếp
Cho đưong tròn tâm O có bán kính R, đường kính AB. Qua điểm A kẻ đường thẳng d vuông góc AB tại A. Trên d lấy điểm C sao cho AC >R. Lấy điểm M thuộc dưong tròn (O) sao cho OM vuông góc với CM tại M. a) Chứng minh 4 điểm A, C, O, M thuộc cùng một đường tròn. b) Gọi K là giao điểm thứ 2 của BC với đường tròn (O). Chứng minh: BC BK = 4R mũ 2 c) Chứng minh: MB // OC d) Chứng minh: góc CMK = gócMBC
GIÚP MIK VỚI Ạ


















