Gọi \(m\) là giá trị nhỏ nhất của hàm số \(y=x^3+\dfrac{27}{x}-18\) trên khoảng \(\left(0;+\infty\right)\). Mệnh đề nào đúng?
A. \(3\le m\le4\)
B. \(2< m< 3\)
C. \(0\le m\le2\)
D. \(m>4\)
Gọi m là giá trị nhỏ nhất của hàm số y = x + 4 x trên khoảng 0 ; + ∞ . Tìm m
![]()
![]()
![]()
![]()
Cho hàm số \(f\left(x\right)=\left|x^2-2x+m\right|\) với \(m\in\left[-2018;2018\right]\). Gọi \(M\) là giá trị nhỏ nhất của hàm số \(f\left(x+\dfrac{1}{x}\right)\) trên tập \(R\backslash\left\{0\right\}\). Số giá trị \(m\) nguyên để \(M\ge2\) là bao nhiêu?
Để giá trị nhỏ nhất của hàm số y = x + 1 x - m trên khoảng (0;+∞) bằng –3 thì giá trị của tham số m là:
A. m = 11 2
B. m = 19 3
C. m = 5
D. m = 7
Đáp án C.
Phương pháp: Sử dung BĐT Cauchy.
Cách giải: 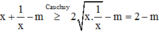
![]()
Để giá trị nhỏ nhất của hàm số y = x + 1 x - m trên khoảng 0 ; + ∞ bằng -3 thì giá trị của tham số m là:
A. m =7
B. m = 19 3 .
C. m = 11 2 .
D. m =5
Để giá trị nhỏ nhất của hàm số y = x + 1 x - m trên khoảng ( 0 ; + ∞ ) bằng -3 thì giá trị của tham số m là:
![]()
![]()
![]()
![]()
Gọi m là giá trị nhỏ nhất của hàm số y = x − 1 + 4 x − 1 trên khoảng 1 ; + ∞ . Tìm m?
A. m = 2
B. m = 5
C. m = 3
D. m = 4
Cho hàm số y=f(x) có đạo hàm xác định trên tập R / - 1 và đồ thị hàm số y=f(x) như hình vẽ. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số y=f(sin2x) trên 0 ; π 2 . Tính P=m.M
A. P=0
B. P=8
C. P=12
D. P=4
Cho hàm số \(y=f\left(x\right)\) liên tục trên R, có đạo hàm \(f'\left(x\right)=x\left(x-1\right)^2\left(x-2\right)\) . Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho hàm số \(y=f\left(\dfrac{x+2}{x+m}\right)\) đồng biến trên khoảng \(\left(10;+\infty\right)\) . Tính tổng các phần tử của S.
Tìm tất cả các giá trị \(m\) để giá trị nhỏ nhất của hàm số:
1/ \(y=\dfrac{x+m}{x-1}\) trên \(\left[2;4\right]\) bằng 3.
2/ \(y=2x^3-3x^2-m\) trên \(\left[-1;1\right]\) bằng 1.
3/ \(y=\left|x^3-3x^2+m\right|\) trên \(\left[0;3\right]\) bằng 2.
Cho hàm số f(x) liên tục trên (0;+ ∞ ) thỏa mãn 3x.f(x) - x 2 f ' ( x ) = 2 f 2 ( x ) , với f(x) ≠ 0, ∀ x ∈ (0;+ ∞ ) và f(1) = 1 3 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Tính M + m.
A. 9 10
B. 21 10
C. 7 3
D. 5 3
Chọn D
Ta có 3x.f(x) -
x
2
f
'
(
x
)
=
2
f
2
(
x
)
![]()
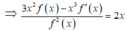
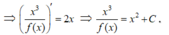
Thay x = 1 vào ta được 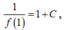 vì f(1) =
1
3
nên suy ra C = 2
vì f(1) =
1
3
nên suy ra C = 2
Nên  Ta có:
Ta có: 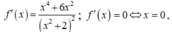
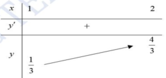
Khi đó, f(x) đồng biến trên [1;2]
Suy ra ![]()
Suy ra ![]()