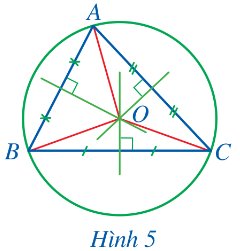
Cho tam giác ABC có O là giao điểm của ba đường trung trực (Hình 5).
a) Các đoạn thẳng OA, OB, OC có bằng nhau không?
b) Đặt R = OA. Đường tròn (O;R) có phải là đường tròn ngoại tiếp tam giác ABC hay không? Vì sao?
Những câu hỏi liên quan
Gọi O là giao điểm của hai đường trung trực ứng với cạnh AB, AC của tam giác ABC (Hình 2).
- Hãy so sánh độ dài của ba đoạn thẳng OA, OB, OC
- Theo em đường trung trực ứng với cạnh BC có đi qua điểm O hay không?
- Ta thấy OA = OB = OC
- Trung trực ứng với cạnh BC đi qua O.
Đúng 0
Bình luận (0)
Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144). Chứng minh:a) Delta OMA Delta OMB và tia MO là tia phân giác của góc NMP;b) O là giao điểm của ba đường phân giác của tam giác MNP.
Đọc tiếp
Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144). Chứng minh:
a) \(\Delta OMA = \Delta OMB\) và tia MO là tia phân giác của góc NMP;
b) O là giao điểm của ba đường phân giác của tam giác MNP.
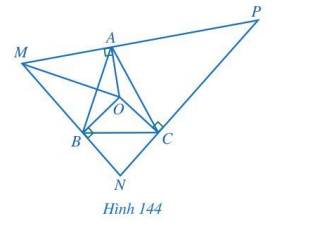
a) O là giao điểm của ba đường trung trực của tam giác ABC nên O cách đều ba đỉnh của tam giác đó hay OA = OB = OC.
Xét hai tam giác vuông OAM và OBM có:
OA = OB;
OM chung.
Vậy \(\Delta OAM = \Delta OBM\)(cạnh huyền – cạnh góc vuông).
Suy ra: \(\widehat {OMA} = \widehat {BMO}\) ( 2 góc tương ứng).
Vậy MO là tia phân giác của góc BMA hay MO là tia phân giác của góc NMP (ba điểm M, A, P thẳng hàng và ba điểm M, B, N thẳng hàng).
b) MO là tia phân giác của góc NMP.
Tương tự ta có:
NO là tia phân giác của góc MNP.
PO là tia phân giác của góc MPN.
Vậy O là giao điểm của ba đường phân giác MO, NO, PO của tam giác MNP.
Đúng 0
Bình luận (0)
A) cho tam giác ABC h. 53 hãy chỉ ra đường trung trực của tam giác đó -hãy vẽ tam giác ABC có độ dài lần lượt là 5cm, 12cm, 13cm, từ đó vẽ các đường trung trực của tam giác nàyB)vẽ tam giác MNP và hai đường trung trực tương ứng với các cạnh MN, MP, - gọi O là giao điểm của đường trung trực nói trên-đo độ dài ba đoạn thẳng nói giao điểm O và ba đỉnh của tam giác em có nhận xét gì về độ dài ba đoạn thẳng nàyC) thực hiện chứng minh tính chất thông qua việc điền vào các chỗ trống dưới đây:-vì O nằm...
Đọc tiếp
A) cho tam giác ABC h. 53 hãy chỉ ra đường trung trực của tam giác đó
-hãy vẽ tam giác ABC có độ dài lần lượt là 5cm, 12cm, 13cm, từ đó vẽ các đường trung trực của tam giác này
B)vẽ tam giác MNP và hai đường trung trực tương ứng với các cạnh MN, MP,
- gọi O là giao điểm của đường trung trực nói trên
-đo độ dài ba đoạn thẳng nói giao điểm O và ba đỉnh của tam giác em có nhận xét gì về độ dài ba đoạn thẳng này
C) thực hiện chứng minh tính chất thông qua việc điền vào các chỗ trống dưới đây:
-vì O nằm trên đường trung trực của đoạn thẳng AC nên OA=OC(1)
-vì O nằm trên đường trung trực của đoạn thẳng AB Nên OA=............(2)
Từ (1) và (2) suy ra . .....=...........(=OA)
Do đó điểm O nằm trên đường.........................của cạnh BC (theo tính chất đường trung trực)
Vậy ba đường trung trực của tam giác ABC cùng đi qua điểm O và ta có OA=OB=OC
Mấy bạn làm giúp mình nha mai mình học rồi sách Venen nha mấy bạn trang 106-107
Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Gọi P,Q, R theo thứ tự là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC
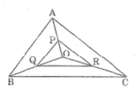
Trong △ OAB, ta có PQ là đường trung bình nên: PQ =1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: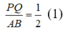 
(1)
Trong △ OAC, ta có PR là đường trung bình nên:
PR = 1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: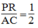 
(2)
Trong △ OBC, ta có QR là đường trung bình nên
QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: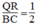 
Từ (1), (2) và (3) suy ra: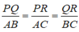 
Vậy △ PQR đồng dạng △ ABC (c.c.c)
Đúng 0
Bình luận (0)
Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Gọi P, Q, R thứ tự là trung điểm của các đoạn thẳng OA, OB, OC
Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC ?
Cho tam giác ABC và điểm O thỏa mãn OA = OB = OC. Chứng minh rằng O là giao điểm của ba đường trung trực của tam giác ABC.
Ta có: OA = OB nên O nằm trên đường trung trực của đoạn thẳng AB ( tính chất đường trung trực của đoạn thẳng)
OB = OC nên O nằm trên đường trung trực của đoạn thẳng BC ( tính chất đường trung trực của đoạn thẳng). (2)
OC = OA nên O nằm trên đường trung trực của đoạn thẳng AC ( tính chất đường trung trực của đoạn thẳng). (3)
Từ (1), (2), và (3) suy ra O là giao điểm của ba đường trung trực của tam giác ABC.
Đúng 0
Bình luận (0)
1) Cho tam giác ABC có các góc đều nhọn, có O là trực tâm. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA và R, S, T lần lượt là trung điểm của OA, OB, OC. a) Chứng minh rằng tứ giác MPTS là hình chữ nhật. b) Chứng minh rằng 3 đoạn thẳng RN, MT, SP bằng nhau và cắt nhau tại trung điểm của mỗi đường. c) Với điều kiện nào của tam giác ABC thì MR=RP=MS.
Gọi O là giao điểm của ba đường trung trực của tam giác ABC (Hình 4). Hãy dùng compa vẽ đường tròn tâm O bán kính OA và cho biết đường tròn này có đi qua hai điểm B và C hay không.
cho tam giác ABC,các đường thẳng AH,BK,CI cắt nhau tại O.Gọi M,N,P là trung điểm lần lượt của AB,BC,CA.Gọi R,S tương ứng là trung điểm của các đoạn OA,OB,OC.
a, CMR các đoạn thẳng RN,MT,SP bằng nhau và cắt nhau tại trung điểm mỗi đường
b, tam giác ABC có thêm điều kiện gì thì các đoạn MG,RP,MS bằng nhau
c,C/m 9 điểm : H;I;K;M;N;P;R;S;T cùng thuộc 1 đường tròn
Cho đường tròn (O ; R) từ điểm A ở ngoài đường tròn (O) vẽ hai tiếp tuyến AB, AC của (O) (B, C là các tiếp điểm); OA cắt BC tại H. a) Chứng minh: tam giác ABC cân và OA là đường trung trực của đoạn BC. b) Chứng minh OH x OA = R²
a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
b: Xét ΔOBA vuông tại B có BH làđường cao
nên OH*OA=OB^2=R^2
Đúng 0
Bình luận (0)