Trong thiết kế logo ở Hình 1, đường tròn đi qua ba đỉnh của tam giác.

Đường tròn đi qua ba đỉnh của tam giác được gọi là gì?
Đâu là định nghĩa của đường tròn ngoại tiếp tam giác?
A.Đường tròn đi qua ba đỉnh của tam giác.
B.Đường tròn có tâm là giao của ba đường phân giác trong tam giác.
C.Đường tròn có tâm là giao của ba đường trung trực trong tam giác.
D.Đường tròn tiếp xúc với ba cạnh của tam giác.
Đáp án : A
chúc bạn học tốt !
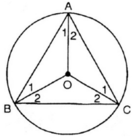
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
Vì tam giác ABC là tam giác đều nên 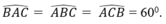
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC
![]()
* Xét tam giác AOB có:
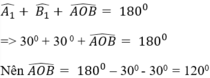
* Tượng tự ta được: ![]()
a) Ta có : ^A = ^B = ^C =60^o ( gt )
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC
Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o
=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o
Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o
b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :
\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)
\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
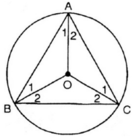
Do ![]()
nên số đo các cung nhỏ AB,BC và AC là:![]()
Suy ra,số đo các cung lớn AB, AC và BC là: 3600 - 1200 = 2400
Vẽ đường tròn đi qua ba đỉnh của tam giác ABC trong các trường hợp sau:
A ^ , B ^ , C ^ đều nhọn
A ^ = 90 o
A ^ > 90 o
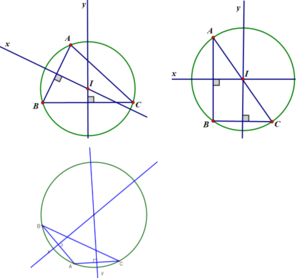
Đường tròn đi qua ba đỉnh của tam giác ABC gọi là đường tròn ngoại tiếp tam giác đó.
Để vẽ đường tròn ta cần:
+ Vẽ đường trung trực y của cạnh BC.
+ Vẽ dường trung trực x của cạnh AB.
+ x cắt y tại I là tâm của đường tròn cần vẽ.
+ Vẽ đường tròn tâm I bán kính IA.
Nhận xét:
- Tam giác nhọn có tâm đường tròn ngoại tiếp nằm trong tam giác.
- Tam giác vuông có tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền (chứng minh bài 56).
- Tam giác tù có tâm đường tròn ngoại tiếp nằm ngoài tam giác.
chứng minh rằng trong một tam giác ba chân đường cao, trung điểm các cạnh,trung điểm đoạn thẳng nối trực tâm của tam giác với các đỉnh cùng đi qua một đường tròn
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua ba đỉnh A, B, C.
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
b) Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
a) Ta có: 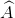 =
=  =
=  =
= 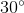 (gt)
(gt)
Suy ra:  =
= 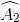 =
= 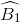 =
= 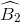 =
= 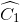 =
= 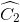 =
=  .
.
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của bà cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC.
Suy ra: 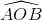 =
= 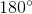 - (
- ( +
+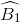 ) =
) = 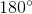 -
- 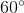 =
= 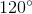
Tương tự ta suy ra 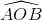 =
= 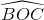 =
= 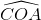 =
= 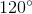 .
.
b) Từ 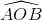 =
= 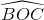 =
= 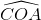 =
= 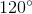 ta suy ra:
ta suy ra:
Cung ABC = BCA = CAB = 240º
Chứng minh rằng tập hợp các điểm cách đều ba đỉnh của một tam giác ABC là đường vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn ngoại tiếp tam giác ABC.
- Lấy một điểm M bất kì trong không gian sao cho MA = MB = MC. Từ M kẻ MO vuông góc với mp(ABC). Các tam giác vuông MOA, MOB, MOC bằng nhau, cho ta OA = OB = OC.
- Suy ra O là tâm đường tròn ngoại tiếp tam giác ABC. Vậy các điểm M cách đều ba đỉnh của tam giác ABC nằm trên đường thẳng d đi qua tâm O của đường tròn ngoại tiếp tam giác ABC và vuông góc với mp(ABC). Ngược lại, lấy một điểm M' ∈ d, nối M'A, M'B, M'C.
- Do M'O chung và OA = OB = OC nên các tam giác vuông M'OA, M'OB, M'OC bằng nhau, cho ta M'A = M'B = M'C.
- Tức là điểm M' cách đều ba đỉnh A, B, C của tam giác ABC.
- Kết luận : Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là đường thẳng vuông góc với mp(ABC) và đi qua tâm của đường tròn ngoại tam giác ABC.
Cho tam giác ABC, kẻ đường cao AH. Gọi I và K theo thứ tự là các điểm đối xứng của H qua các cạnh AB và AC. Biết AH = \(2\sqrt{5}\) cm; BH = 4cm; CH = 5cm.
1) Tìm tâm và bán kính của đường tròn đi qua ba đỉnh A, B, C
2) Chứng minh H nằm trên đường tròn đường kính HK
1: \(AB=\sqrt{AH^2+HB^2}=\sqrt{20+16}=6\left(cm\right)\)
\(AC=\sqrt{AH^2+HC^2}=3\sqrt{5}\)
Vì AB^2+AC^2=BC^2
nên ΔABC vuông tại A
=>tâm là trung điểm của BC
Bán kính là BC/2=4,5cm
2:Gọi Llà trung điểm của HK
Xét (L) có
HK là đường kính
nên H thuộc (L)
Cho tam giác ABC, vuông tại A đường cao AH. Biết AH = 2 căn 3, góc BAH = 60 độ. Tính bán kính đường tròn đi qua ba đỉnh của tam giác ABC
Xét \(\Delta\) vuông tại H \(ABH\) có :
\(tan\widehat{BAH}=tan60^o=\dfrac{BH}{AH}\Rightarrow BH=AH.tan60^o=2\sqrt[]{3}.\sqrt[]{3}=6\)
Xét \(\Delta\) vuông tại H \(ACH\) có :
\(\widehat{HAC}=90^o-\widehat{BAH}=90^o-60^o=30^o\)
\(tan\widehat{HAC}=tan30^o=\dfrac{CH}{AH}\Rightarrow CH=AH.tan30^o=2\sqrt[]{3}.\dfrac{1}{\sqrt[]{3}}=2\)
Tâm đường tròn ngoại tiếp tam giác vuông ABC là trung điểm BC
\(\Rightarrow\) Bán kính đường tròn này là :
\(R=\dfrac{BC}{2}=\dfrac{BH+CH}{2}=\dfrac{6+2}{2}=4\)
Cho tam giác ABC, kẻ đường cao AH. Gọi I, K là các điểm đối xứng của H qua các cạnh AB,AC. Biết AH=2√5, BH=4,CH=5cm. a.tìm tâm và bán kính của đường tròn đi qua ba đỉnh A,B,C. b. Chứng minh H nằm trên đường tròn đường kính IK, từ đó suy ra các điểm B,C thuộc miền ngoài của đường kính IK. Giúp em một bài hoàn chỉnh có cả hình để em tham khảo với mn ơi
a: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
HB/HA=HA/HC
=>ΔHBA đồng dạng với ΔHAC
=>góc HBA=góc HAC
=>góc HBA+góc HCA=90 độ
=>góc BAC=90 độ
=>ΔBAC nội tiếp đường tròn đường kính BC
Tâm là trung điểm của BC
Bán kính là R=BC/2=4,5
b: Gọi giao của HI với AB là M, HK với AC là N
H đối xứng I qua AB
=>HI vuông góc AB tại M
H đối xứng K qua AC
=>HK vuông góc AC tại N
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
=>góc MHN=90 độ
=>góc IHK=90 độ