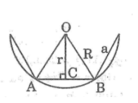
Xác định tâm và bán kính đường tròn nội tiếp tam giác đều MNP có độ dài cạnh bằng 8 cm.

Những câu hỏi liên quan
Cho MNP là tam giác đều cạnh dài 9 cm. Bán kính đường tròn ngoại tiếp tam giác MNP bằng:
Bán kính đường tròn ngoại tiếp tam giác MNP bằng: 3 3 cm
Đúng 0
Bình luận (0)
Bài 5 (1 điểm): Cho tam giác MNP vuông tại M, có MN = 6 cm, MP = 8 cm. Chứng minh rằng các
đỉnh M, N, P cùng thuộc một đường tròn. Hãy xác định tâm và tính độ dài bán kính của đường tròn
đó.
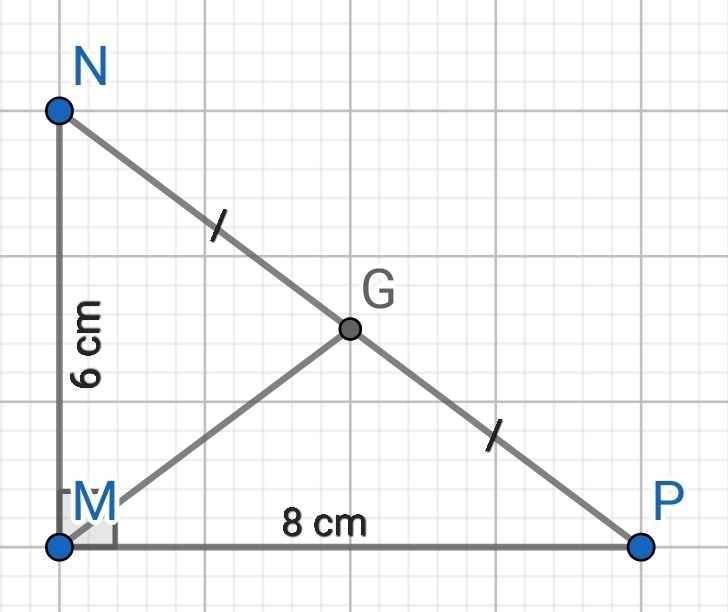
Ta có:
∆MNP vuông tại M
⇒ NP² = MP² + MN² (Pytago)
= 8² + 6² = 100
⇒ NP = 10 (cm)
Gọi G là trung điểm của NP
⇒ MG là đường trung tuyến ứng với cạnh huyền NP của ∆MNP
⇒ MG = NG = PG = NP : 2 = 5 (cm)
⇒ M, N, P cùng thuộc đường tròn tâm G, bán kính MG = 5 cm
Đúng 1
Bình luận (0)
Stshdtgfdrsgettgstgefdfe📱📱📱📱📱📱💻📱📱📱📱📱📱📱📱💻💻💻💻💻💻📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱🖍️🖍️📱📱📱📱📱📱📱📱📱📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱📱💻💻📱💻📱💻📱💻📱📱💻💻📱📱💻📱💻📱💻📱💻📱📱💻📱📱📱📱📱📱📱💻📱💻📱📱💻📱📱📱💻📱💻📱📱📱📱📱📱💻💻💻💻📱📱📱📱
Đúng 0
Bình luận (0)
một tam giác cân có cạnh đáy 16cm, cạnh bên 10cm. Tính độ dài các bán kính đường tròn nội tiếp, ngoại tiếp tam giác và khoảng cách giữa các tâm của hai đường tròn đó
ác định tâm và bán kính đường tròn ngoại tiếp tam giác đều có cạnh bằng a
làm nhanh tui tích
Tâm là giao điểm của ba đường trung tuyến
Bán kính là bằng 2/3 của độ dài đường trung tuyến
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, đường cao AH bằng 10cm, đường cao BK bằng 12cm. Độ dài cạnh đáy BC là cm.
Cho tam giác ABC cân tại A có BC = 24cm , AC = 20cm.
Độ dài bán kính đuờng tròn tâm O nội tiếp tam giác ABC là cm.
BC và AK cắt BC tại H.Ta có HB=HC (AK là trung trực của BC)
=>HC=BC/2.
AH=√(AC²-CH²);
∆ACH~∆COH (tam giác vuông chung góc nhọn tại O)
=>AH/AC=HC/CO=>CO=AC.HC/AH.
=20.12/√(20²-12²)=20.12/16=15.
Đúng 0
Bình luận (0)
Gọi AH, BK là hai đường cao, có AH = 10; BK = 12
thấy hai tgiác CAH và CBK đồng dạng => CA/AH = CB/BK
=> CA/10= 2CH/12 => CA = 2,6.CH (1)
mặt khác áp dụng pitago cho tgiac vuông HAC:
CA² = CH² + AH² (2)
thay (1) vào (2): 2,6².CH² = CH² + 102
=> (2,6² - 1)CH² = 102=> CH = 10 /2,4 = 6,5
=> BC = 2CH = 13 cm
Đúng 0
Bình luận (1)
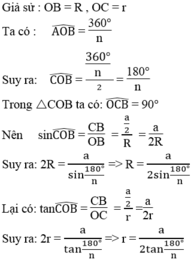
Cho một đa giác đều n cạnh có độ dài mỗi cạnh là a. Hãy tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp đa giác đều đó
ho tam giác MNP có MN=MP nội tiếp đường tròn tâm O, các đường cao MA, NB, PC cắt nhau tại H.
a, cm tứ giác MPHC là tứ giác nội tiếp. xác định tâm I của đường tròn ngoại tiếp tức giác đó
b, cm MC. MP= MH.MA
C, cm AB là tiếp tuyến đường tròn tâm I
cho tam giác MNP có MN=MP nội tiếp đường tròn tâm O, các đường cao MA, NB, PC cắt nhau tại H.
a, cm tứ giác MBHC là tứ giác nội tiếp. xác định tâm I của đường tròn ngoại tiếp tức giác đó
b, cm MC. MP= MH.MA
C, cm AB là tiếp tuyến đường tròn tâm I
a: Xét tứ giác MBHC có
\(\widehat{MBH}+\widehat{MCH}=180^0\)
Do đó: MBHC là tứ giác nội tiếp
b: Sửa đề: \(MC\cdot MP=MB\cdot MN\)
Xét ΔMCP vuông tại C và ΔMBN vuông tại B có
\(\widehat{BMN}\) chung
Do đó: ΔMCP\(\sim\)ΔMBN
Suy ra: MC/MB=MP/MN
hay \(MC\cdot MN=MB\cdot MP\)
Đúng 0
Bình luận (0)
cho tam giác MNP có MN=MP nội tiếp đường tròn tâm O, các đường cao MA, NP, PC cắt nhau tại H. a, cm tứ giác MPHC là tứ giác nội tiếp. xác định tâm I của đường tròn ngoại tiếp tức giác đó
b, cm MC. MP= MH.MA
C, cm AB là tiếp tuyến đường tròn tâm I
sao lại đường cao NP bạn ? xem lại đề nhé
Đúng 0
Bình luận (3)
Xét tứ giác MBHC có :
^MCH + ^MBH = 1800
mà 2 góc này đối
Vậy tứ giác MBHC là tứ giác nt 1 đường tròn
Đúng 0
Bình luận (0)