Trong bảng số liệu sau có một số liệu không chính xác. Hãy tìm số liệu đó và sửa lại cho đúng.

Cho bảng số liệu sau
GDP và tốc độ tăng trưởng của GDP của Nhật Bản giai đoạn 2010 – 2014

Từ số liệu ở nảng trên, hãy cho biết nhận định nào sau đây chính xác về tốc độ tăng trưởng GDP của Nhật Bản trong giai đoạn 2010 - 2014?
A. thấp và không ổn định
B. thấp và tăng đều
C. cao và ổn định
D. cao nhưng giảm đều
Dựa vào bảng số liệu đã cho, nhận xét chính xác về tốc độ tăng trưởng GDP của Nhật Bản trong giai đoạn 2010 - 2014 là thấp và không ổn định vì tốc độ tăng trưởng luôn dưới 5% và tăng giảm không đều qua các năm => Chọn đáp án A
Cho bảng số liệu:
THU NHẬP BÌNH QUÂN ĐẦU NGƯỜI/THÁNG Ở MỘT SỐ VÙNG CỦA NƯỚC TA, GIAI ĐOẠN 2004 - 2016
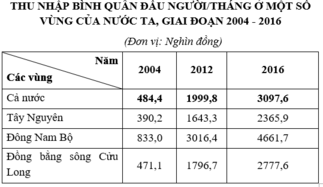
Theo bảng số liệu, nhận định nào sau đây không chính xác về thu nhập bình quân đầu người/tháng ở một số vùng của nước ta, giai đoạn 2004 – 2016?
A. Thu nhập bình quân đầu người của nước ta có xu hướng tăng lên
B. Thu nhập bình quân đầu người có sự phân hoá giữa các vùng
C. Vùng có kinh tế phát triển có thu nhập cao và ngược lại
D. Các vùng miền núi có thu nhập cao hơn các vùng đồng bằng.
Cho bảng số liệu:
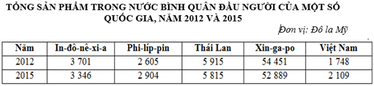
Căn cứ vào bảng số liệu, cho biết nhận xét nào sau đây không đúng về tốc độ tăng trưởng tổng sản phẩm trong nước bình quân đầu người của một số quốc gia, năm 2012 và 2015?
A. Xin-ga-po giảm chậm hơn In-đô-nê-xi-a.
B. Phi-líp-pin tăng chậm hơn Việt Nam.
C. Xin-ga-po tăng nhiều nhất.
D. Thái Lan giảm chậm nhất.
Đáp án C
Cách tính tốc độ tăng trưởng:
+ Chọn năm đầu tiên là năm mốc và năm mốc sẽ là 100%.
+ Tốc độ tăng trưởng = số liệu năm cuối : số liệu năm đầu x 100 (đơn vị: %).
Từ công thức trên ta tính được tốc độ tăng trưởng của các ngành và so sánh:
+ In-đô-nê-xi-a: 90,4%.
+ Thái Lan: 98,2%.
+ Việt Nam: 120,7%.
+ Phi-líp-pin: 111,5%.
+ Xin-ga-po: 91,15%.
Như vậy, ta thấy Việt Nam có tốc độ tăng trưởng nhanh nhất, tiếp đến là Phi-lip-pin. Còn Thái Lan, Xin-ga-po và In-đô-nê-xi-a có tốc độ tăng trưởng giảm, trong đó In-đô-nê-xi-a giảm nhiều nhất, Thái Lan giảm chậm nhất.
Cho bảng số liệu:

Căn cứ vào bảng số liệu, cho biết nhận xét nào sau đây không đúng về chỉ số phát triển con người của một số quốc gia, năm 2014 và 2015?
A. Nhật Bản tăng nhiều hơn Trung Quốc.
B. Trung Quốc tăng nhiều hơn Hàn Quốc.
C. Hàn Quốc tăng nhiều hơn Nhật Bản.
D. Việt Nam tăng nhiều hơn Hàn Quốc.
Đáp án C
- Công thức: Chỉ số HDI tăng lên = Chỉ số HDI năm sau - Chỉ số HDI năm trước
Ví dụ: Chỉ số HDI tăng lên của Nhật Bản = 0,903 – 0,891 = 0,012.
- Tương tự, ta tính được kết quả sau:
+ Hàn Quốc: 0,003.
+ Việt Nam: 0,017.
+ Trung Quốc: 0,011.
Như vậy, ta thấy Việt Nam tăng nhiều nhất, tiếp theo là Nhật Bản, Trung Quốc và tăng ít nhất là Hàn Quốc.
=> Hàn Quốc tăng ít hơn Nhật Bản (0,003 < 0,012)
=> Nhận xét Hàn Quốc có chỉ số HDI tăng nhiều hơn Nhật Bản là không đúng
Cho bảng số liệu: Lượng mưa, lượng bốc hơi và cân bằng ẩm của một số địa điểm (Đơn vị: mm)
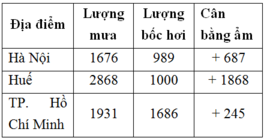
Nhận xét nào sau đây không đúng với bảng số liệu trên?
A. Lượng mưa và lượng bốc hơi tăng dần từ Bắc vào Nam
B. Hà Nội có lượng mưa và lượng bốc hơi nhỏ nhất
C. Huế có lượng mưa và cân bằng ẩm lớn nhất
D. TP. Hồ Chí Minh có lượng bốc hơi lớn nhất và cân bằng ẩm nhỏ nh
Dựa vào bảng số liệu đã cho, nhận xét thấy lượng mưa cao nhất ở Huế - miền Trung vì vậy không thể nhận xét Lượng mưa và lượng bốc hơi tăng dần từ Bắc vào Nam => nhận xét A không đúng => Chọn đáp án A
Cho bảng số liệu:
THU NHẬP BÌNH QUÂN ĐẦU NGƯỜI/THÁNG Ở MỘT SỐ VÙNG CỦA NƯỚC TA, GIAI ĐOẠN 2004 - 2016
(Đơn vị: Nghìn đồng)
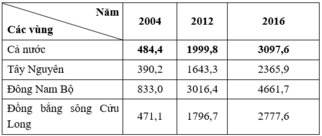
Theo bảng số liệu, nhận định nào sau đây không chính xác về thu nhập bình quân
đầu người/tháng ở một số vùng của nước ta, giai đoạn 2004 – 2016?
A. Thu nhập bình quân đầu người của nước ta có xu hướng tăng lên.
B. Thu nhập bình quân đầu người có sự phân hoá giữa các vùng.
C. Vùng có kinh tế phát triển có thu nhập cao và ngược lại.
D. Các vùng miền núi có thu nhập cao hơn các vùng đồng bằng.
Cho bảng số liệu:
THU NHẬP BÌNH QUÂN ĐẦU NGƯỜI/THÁNG Ở MỘT SỐ VÙNG CỦA NƯỚC TA, GIAI ĐOẠN 2004 - 2016
(Đơn vị: Nghìn đồng)
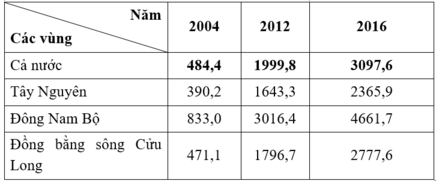
Theo bảng số liệu, nhận định nào sau đây không chính xác về thu nhập bình quân đầu người/tháng ở một số vùng của nước ta, giai đoạn 2004 – 2016?
A. Thu nhập bình quân đầu người của nước ta có xu hướng tăng lên
B. Thu nhập bình quân đầu người có sự phân hoá giữa các vùng
C. Vùng có kinh tế phát triển có thu nhập cao và ngược lại
D. Các vùng miền núi có thu nhập cao hơn các vùng đồng bằng
Cho bảng số liệu sau:
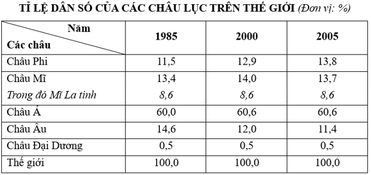
Nhận xét nào sau đây không đúng với bảng số liệu trên?
A. Tỉ lệ dân số châu Phi và châu Á có xu hướng tăng, trong đó nhiều nhất thuộc về châu Á.
B. Dân số châu Mĩ tăng từ 13,4% năm 1985 lên 14% năm 2000 nhưng đến 2005 giảm xuống còn 13,7%.
C. Tỉ trọng dân số châu Âu có xu hướng giảm mạnh từ 14,6% năm 1985 xuống 11,4% năm 2005.
D. Châu Đại Dương là châu lục duy nhất dân số không thay đổi, giữ ở mức 0,5%.
Đáp án A
- Công thức: Tỉ lệ dân số tăng lên = Tỉ lệ dân số năm cuối – Tỉ lệ dân số năm gốc (đơn vị: %).
- Từ công thức trên, ta tính được:
+ Châu Phi tăng thêm 2,3%.
+ Châu Mĩ tăng thêm 0,3%.
+ Châu Á tăng thêm 0,6%.
+ Châu Âu giảm 3,2%.
+ Châu Đại Dương ổn định, không tăng và không giảm.
Như vậy:
- châu Phi tăng nhiều nhất, tiếp đến là châu Á, châu Mĩ. Trong khi đó châu Âu có tỉ trọng giảm và châu Đại Dương không có sự thay đổi.
- Tỉ trọng của châu Á là lớn nhất (60,6% - 2005), đứng thứ 2 là châu Phi, tiếp đến là châu Mĩ, châu Âu và cuối cùng chiếm tỉ trọng nhỏ nhất là châu Đại Dương.
Kết luận: Châu Á tăng nhiều nhất là sai nên ý A là không đúng.
Cho bảng số liệu sau:

Nhận định nào sau đây không đúng với bảng số liệu trên?
A. Hiệp ước tự do thương mại Bắc Mĩ có GDP bình quân đầu người cao nhất.
B. Liên Minh châu Âu có GDP bình quân đầu người thấp nhất.
C. Hiệp hội các nước Đông Nam Á có số dân đứng thứ nhất và GDP đứng thứ 3.
D. Các khu vực có số dân, GDP không đồng đều giữa các khu vực.
Đáp án B
Cần tìm ra các phương án đúng để biết được phương án không đúng.
Nhìn vào bảng có thể nhận thấy số dân, GDP không đồng đều giữa các khu vực, như vậy ý D đúng.
Sắp xếp Số dân theo thứ tự giảm dần: Hiệp hội các nước Đông Nam Á, Liên Minh châu Âu, Hiệp ước tự do thương mại Bắc Mĩ. GDP theo thứ tự giảm dần: Hiệp ước tự do thương mại Bắc Mĩ., Liên Minh châu Âu, Hiệp hội các nước Đông Nam Á nên ý C đúng.
Tính GDP bình quân đầu người:
- Công thức: GDP bình quân đầu người = GDP : người (đơn vị: USD/người).
- Từ công thức trên, tính được kết quả sau:
+ Hiệp ước tự do thương mại Bắc Mĩ: 42278 USD/người (cao nhất).
+ Liên Minh châu Âu: 35000 USD/người.
+ Hiệp hội các nước Đông Nam Á: 29995 USD/người (thấp nhất).
Như vậy ý A đúng và ý B sai.
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)