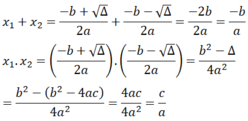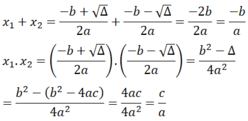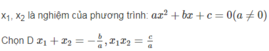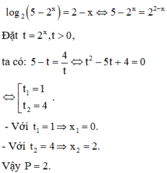Từ kết quả HĐ1, hãy tính x1 + x2 và x1x2.

Những câu hỏi liên quan
2x^2-3x-1 Không giải phương trình hãy tính tổng tích A=1/x1-3+1/x2-3 B=x1²x2-4-x1x2+x1x2² C=1-x1²-x2² D=x1³x2³+x1³+x2³
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1x_2=-\dfrac{1}{2}\end{matrix}\right.\)
\(A=\dfrac{1}{x_1-3}+\dfrac{1}{x_2-3}=\dfrac{x_2-3+x_1-3}{\left(x_1-3\right)\left(x_2-3\right)}=\dfrac{x_1+x_2-6}{x_1x_2-3\left(x_1+x_2\right)+9}\)
\(=\dfrac{\dfrac{3}{2}-6}{-\dfrac{1}{2}-3.\dfrac{3}{2}+9}=...\) (em tự bấm máy)
\(B=x_1^2x_2-4-x_1x_2+x_1x_2^2=x_1x_2\left(x_1+x_2\right)-4-x_1x_2\)
\(=-\dfrac{1}{2}.\dfrac{3}{2}-4-\left(-\dfrac{1}{2}\right)=...\)
\(C=1-\left(x_1^2+x_2^2\right)=1-\left(x_1+x_2\right)^2+2x_1x_2=1-\left(\dfrac{3}{2}\right)^2+2.\left(-\dfrac{1}{2}\right)=...\)
\(D=x_1^3x_2^3+x_1^3+x_2^3=\left(x_1x_2\right)^3+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
\(=\left(-\dfrac{1}{2}\right)^3+\left(\dfrac{3}{2}\right)^3-3.\left(-\dfrac{1}{2}\right).\dfrac{3}{2}=...\)
Đúng 1
Bình luận (0)
Hãy tính
x
1
+
x
2
,
x
1
x
2
.
x
1
−
b
+
Δ
2...
Đọc tiếp
Hãy tính x 1 + x 2 , x 1 x 2 .
x 1 = − b + Δ 2 a , x 2 = − b − Δ 2 a
Hãy tính x1 + x2, x1x2.
x
1
-
b
+
∆
2
a
,
x
2
-
b
-
∆
2...
Đọc tiếp
Hãy tính x1 + x2, x1x2.
x 1 = - b + ∆ 2 a , x 2 = - b - ∆ 2 a
cho x2 - 2(m + 1)x + m2 + m - 1 = 0
tìm các giá trị của m để pt có nghiệm
trong trường hợp có nghệm là x1 và x2 hãy tính x1 + x2, tính x1x2 và (x1)2 + (x2)2 theo m
\(\Delta'=\left(m+1\right)^2-\left(m^2+m-1\right)\ge0\)
\(\Leftrightarrow m+2\ge0\Rightarrow m\ge-2\)
Khi đó theo hệ thức Viet : \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4\left(m+1\right)^2-2\left(m^2+m-1\right)=2m^2+6m+6\)
Đúng 4
Bình luận (0)
x2 - 2(m + 1)x + m2 + m - 1 = 0
\(\Delta\) = [-2(m + 1)]2 - 4.1.(m2 + m - 1) = 4(m2 + 2m + 1) - 4m2 - 4m + 4 = 4m2 + 8m + 4 - 4m2 - 4m + 4 = 4m + 8
Để pt có nghiệm thì \(\Delta\) \(\ge\) 0 \(\Leftrightarrow\) 4m + 8 \(\ge\) 0 \(\Leftrightarrow\) m \(\ge\) -2
Với m \(\ge\) -2 ta có:
x1 = \(\dfrac{2\left(m+1\right)+\sqrt{4m+8}}{2}=m+1+\sqrt{m+2}\)
x2 = \(\dfrac{2\left(m+1\right)-\sqrt{4m+8}}{2}=m+1-\sqrt{m+2}\)
x1 + x2 = m + 1 + \(\sqrt{m+2}\) + m + 1 - \(\sqrt{m+2}\) = 2m + 2
x1x2 = (m + 1 + \(\sqrt{m+2}\))(m + 1 - \(\sqrt{m+2}\)) = (m + 1)2 - m - 2 = m2 + 2m + 1 - m - 2 = m2 + m - 1 = \(\left(m+\dfrac{1-\sqrt{5}}{2}\right)\left(m+\dfrac{1+\sqrt{5}}{2}\right)\)
(x1)2 + (x2)2 = (m + 1 + \(\sqrt{m+2}\))2 + (m + 1 - \(\sqrt{m+2}\))2 = (x1 + x2)2 - 2x1x2 = (2m + 2)2 - 2(m2 + m - 1) = 4m2 + 8m + 4 - 2m2 - 2m + 2 = 2m2 + 6m + 6 = 2(m2 + 3m + 3)
Chúc bn học tốt!
Đúng 2
Bình luận (0)
Tính m biết x1+x2=-2m và x1x2=4 và A=x1-x2
Giả sử
x
1
,
x
2
là hai nghiệm của phương trình a
x
2
+ bx + c 0, ( ).Điều nào sau đây đúng?
A
.
x
1
+...
Đọc tiếp
Giả sử x 1 , x 2 là hai nghiệm của phương trình a x 2 + bx + c = 0, ( ).
Điều nào sau đây đúng?
A . x 1 + x 2 = b a , x 1 x 2 = c a B . x 1 + x 2 = - b a , x 1 x 2 = - c a C . x 1 + x 2 = b a , x 1 x 2 = - c a D . x 1 + x 2 = - b a , x 1 x 2 = c a
Cho phương trình: 3x2 – 5x – 6 = 0 có 2 nghiệm x1, x2. Không giải phương trình, hãy tính giá trị của biểu thức sau: A=1-( \(\dfrac{x1-x2}{x1x2}\))2
Biết phương trình
log
2
5
-
2
x
2
-
x
có hai nghiệm
x
1
,
x
2
. Tính
P
x
1
+
x
2
+
x
1...
Đọc tiếp
Biết phương trình log 2 5 - 2 x = 2 - x có hai nghiệm x 1 , x 2 . Tính P = x 1 + x 2 + x 1 x 2
A. P = 2
B. P = 3
C. P = 4
D. P = 9
Giải sử phương trình -x^2+(6-m)x-2m+3=0 có hai nghiệm x1, x2. Tính x1+x2+x1x2 theo m.
Biết rằng phương trình
2
ln
(
x
+
2
)
+
ln
4
ln
x
+
4
ln
3
có hai nghiệm phân biệt
x
1
,
x
2
(
x
1
x
2
). Tính giá trị của
P
x...
Đọc tiếp
Biết rằng phương trình 2 ln ( x + 2 ) + ln 4 = ln x + 4 ln 3 có hai nghiệm phân biệt x 1 , x 2 ( x 1 < x 2 ). Tính giá trị của P = x 1 x 2 ?
A. 64
B. 4
C. 1 64
D. 1 4