Cho dây AB không qua tâm của đường tròn (O). Gọi A' và B' là hai điểm lần lượt đối xứng với A và B qua (O). Hỏi đường trung trực của A'B' có phải là trục đối xứng của (O) hay không? Tại sao?

Những câu hỏi liên quan
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng: AB ⊥ KB
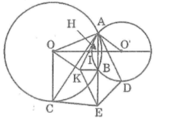
Gọi H là giao điểm của AB và OO’
Vì OO’ là đường trung trực của AB nên OO’ ⊥ AB tại H
Ta có: HA = HB
I là trung điểm của OO’ nên IH ⊥ AB (1)
Trong tam giác ABK, ta có:
HA = HB (chứng minh trên)
IA = IK (tính chất đối xứng tâm)
Suy ra IH là đường trung bình của tam giác ABK
Suy ra IH // BK (2)
Từ (1) và (2) suy ra: AB ⊥ KB
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng: Bốn điểm A, C, E, D cùng nằm trên một đường tròn
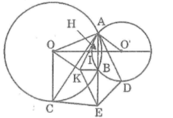
Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3
Đúng 0
Bình luận (0)
Cho 2 đường tròn tâm O và O cắt nhau tại A và B dây AC của (O) tiếp xúc với (O ) tại A. Dây AD của (O ) tiếp xúc với (O) tại A Gọi K là điểm đối xứng với A qua trung điểm I của OO . E là điểm đối xứng với A qua B. Chứng minh rằng:
a) AB vuông góc với KB
b) 4 điểm A;C;D;E nằm trên một đường tròn
Cho 2 đường tròn tâm O và O cắt nhau tại A và B dây AC của (O) tiếp xúc với (O ) tại A. Dây AD của (O ) tiếp xúc với (O) tại A Gọi K là điểm đối xứng với A qua trung điểm I của OO . E là điểm đối xứng với A qua B. Chứng minh rằng:
a) AB vuông góc với KB
b) 4 điểm A;C;D;E nằm trên một đường tròn
Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O) tại A. Dây AD của đường tròn (O) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO, E là điểm đối xứng với A qua B. Chứng minh rằng :
a) ABperp KB
b) Bốn điểm A, C, E, D nằm trên cùng một đường tròn
Đọc tiếp
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O') tại A. Dây AD của đường tròn (O') tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO', E là điểm đối xứng với A qua B. Chứng minh rằng :
a) \(AB\perp KB\)
b) Bốn điểm A, C, E, D nằm trên cùng một đường tròn
cho hai đường tròn (O) và (O') cắt nhau tại A và B.Trên (O) và (O') lần luọt lấy C và D sao cho AC, AD là tiếp tuyến của (O), (O'). Gọi E là điểm đối xứng với A qua trung điểm I của đoạn thẳng OO' và G là điểm đối xứng với A qua B. CMR: A, C, G, D cùng thuộc một đường tròn
cho đường tròn tâm o có đk ab và điểm m thuộc đường tròn. vẽ điểm n đối xứng với a qua m. đoạn thẳng bn cắt đường tròn o tại c. gọi e là giao điểm của đh thẳng ac và bm.
-cm tam giác amb vuông và e là trực tâm của tam giác anb.
-gọi f là điểm đối xứng với e qua m. chứng minh af là tiếp tuyến
-Chứng minh 2mf.mb=nc.nb
mình cần gấp
a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) đường kính AB. Gọi M là một điểm nằm giữa A và B. Qua M vẽ dây CD vuông góc với AB. Lấy điểm E đối xứng với A qua M. a) Tứ giác ACED là hình gì? Tại sao? b) Chứng minh rằng AB là đường trung trực của CD. c) Cho R = 6,5 cm và MA = 4 cm. Tính CD và diện tích tứ giác ACBD
cho hai đường tròn (O) và (O') cắt nhau tại A và B .Dây AC của đường tròn (O) tiếp xúc với đường tròn (O') tại A.Dây AD của đường tròn (O') tiếp xúc với đường tròn (O) tại A.Gọi K là điểm đối xứng với A qua trung điểm I của OO' ,E là điểm đối xứng với A và B.cmr:
a)AB vuông góc với KB
b)Bốn điểm A,C,E,D nằm trên cùng một đường tròn
Cho đường tròn tâm O đường kính MN, dây cung AB vuông góc với MN tại điểm I nằm giữa O, N. Gọi K là một điểm thuộc dây AB nằm giữa A, I. Các tia MK, NK cắt đường tròn tâm O theo thứ tự tại C,D. Gọi E, F, H lần lượt là hình chiếu của C trên các đường thẳng AD, AB, BD. Chứng minh rằng:a) AC.HF AD.CFb) F là trung điểm của EHc) Hai đường thẳng DC và DI đối xứng nhau qua đường thẳng DN.
Đọc tiếp
Cho đường tròn tâm O đường kính MN, dây cung AB vuông góc với MN tại điểm I nằm giữa O, N. Gọi K là một điểm thuộc dây AB nằm giữa A, I. Các tia MK, NK cắt đường tròn tâm O theo thứ tự tại C,D. Gọi E, F, H lần lượt là hình chiếu của C trên các đường thẳng AD, AB, BD. Chứng minh rằng:
a) AC.HF = AD.CF
b) F là trung điểm của EH
c) Hai đường thẳng DC và DI đối xứng nhau qua đường thẳng DN.















