1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b hoặc AB = c, BC = a và không sử dụng định lí Pythagore (H.4.21).
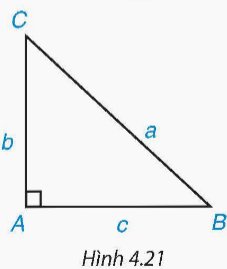
2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Sử dụng tích vô hướng, chứng minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi \(B{C^2} = A{B^2} + A{C^2}\).
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
Ta có: \(\widehat A = {90^o}\) (tam giác ABC vuông tại A) \( \Leftrightarrow \cos A = \cos {90^o} = 0\)
\( \Leftrightarrow B{C^2} = A{B^2} + A{C^2}\) (đpcm)
a) Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', AC > A'C'. Không sử dụng định lí Pitago, chứng minh rằng BC > B'C'
b) Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', BC > B'C'. Không sử dụng định lí Pitago, chứng minh rằng AC > A'C'
a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.
Cho tam giác ABC vuông tại A có AB<AC. Trên cạnh AC lấy điểm H. Qua C kẻ đường thẳng vuông góc với đường thẳng BH tại D.
a) Chứng minh HB.HD=HA.HC
b) Chứng minh tam giác ADH đồng dạng tam giác BCH
c) Kẻ HK vuông góc BC tại K. Chứng minh H cách đều ba cạnh của tam giác ADK.
a) Xét ΔCDH vuông tại D và ΔBAH vuông tại A có
\(\widehat{CHD}=\widehat{BHA}\)(hai góc đối đỉnh)
Do đó: ΔCDH\(\sim\)ΔBAH(g-g)
Suy ra: \(\dfrac{HD}{HA}=\dfrac{HC}{HB}\)
hay \(HB\cdot HD=HA\cdot HC\)
b) Ta có: \(\dfrac{HD}{HA}=\dfrac{HC}{HB}\)(cmt)
nên \(\dfrac{HD}{HC}=\dfrac{HA}{HB}\)
Xét ΔADH và ΔBCH có
\(\dfrac{HD}{HC}=\dfrac{HA}{HB}\)(cmt)
\(\widehat{AHD}=\widehat{BHC}\)(hai góc đối đỉnh)
Do đó: ΔADH\(\sim\)ΔBCH(c-g-c)
cho tam giác ABC cân tại B, có góc B = 400 ,BA = 3 cm.hãy nêu cách vẽ tam giác cân ABC và tính hai cạnh BC và cạnh AC?
2) Cho tam giác ABC cân tại C .CA = CB = 10 cm. AB = 12 cm.kẻ CI vuông góc với AB
a) chững minh IA = IB
b) Tính IC
cho tam giác abc vuông tại a và có chu vi là 120. biết độ dài cách ac bằng 75% cạnh ab. độ dài cách bc bằng 5/7 tổng độ dài hai cách ac và bc. hãy tính chiều cao ah tương ứng với cách bc của hình tam giác abc?
chu vi cua hinh tam giac a,b,c bang 1m65cm tong hai canh ab va ac bang 9cm, hoi canh bc dai bao nhieu cm la
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
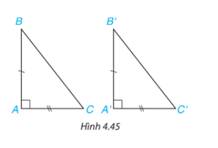
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
Bài 2: (2,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết cạnh AH = 12 , CH = 6cm a) Tính độ dài cạnh BH,AB. b) Gọi M hình chiếu vuông góc kẻ từ H đến AB. Chứng minh: BM = (A * B ^ 3)/(B * C ^ 2) c) Hãy giải tam giác AHC vuông tại H. (Kết quả số đo góc làm tròn đến phút, độ dài làm tròn đến chữ số thập phân thứ hai).
Cho tam giác ABC vuông tại A có AB : AC = 4 : 5 và đường cao AH bằng 12cm. Khi đó độ dài đoạn thẳng HB bằng
A. 6cm; B. 9,6cm; C. 12cm; D. 15cm.
Hãy chọn phương án đúng.
*Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác ABC vuông tại A có đường cao AH:
AB = c, AC = b, BC = a, AH = h, BH = c’, CH = b’.
Hướng dẫn:
∆
ABC ∼
∆
HBA nên 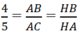
Suy ra HB = 4/5HA = 48/5 = 9,6. Chọn B.
Nêu định lí Pi-ta-go trong tam giác vuông ABC vuông tại A,biết BC là cạnh huyền.(ko có hình nên nói vậy cho dễ hiểu.)Từ đó,áp dụng tính AB,AC.
Định lí Pitago:Bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại.
Từ đề bài, ta có 2 cạnh góc vuông là: AB, AC
Cạnh huyền là: BC
Ta có hệ thức từ định lí Pitago: \(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\Rightarrow AB=\sqrt{BC^2-AC^2}\)
\(\Rightarrow AC^2=BC^2-AB^2\Rightarrow AC=\sqrt{BC^2-AB^2}\)
Chúc bạn buổi tối vui vẻ nha ^^
ai biết giải giúp minh với:
Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minh
a,tứ giác HECD nội tiếp
b,Tia DA là tia phân giác góc EDK
Cây 2:cho tam giác ABC vuông tai A,biết ab=6cm,ac=8cm
A.tính bc
B,kẻ đường cao AH,tính Ah
Câu 3:Cho tam giác abc vuông tại A,BIẾT AC=4cm,Bc=5cm.
A,Tính cạnh AB
B,kẻ đường cao AH,TÍNH AH
Câu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB=12CM,AC=5CM.tính BH,CH
Câu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC=18cm,BH=6cm.Tính độ dài các cạnh AB,AC
Cau 6:Cho tam giác ABC,vuông tại A,biết AB=4cm,đường cao AH=2CM,tính các góc và các cạnh còn lại cua tam giac.?
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ