Cho đường tròn (O) và điểm C nằm nên ngoài đường tròn. Qua C kẻ tiếp tuyên CA, CB với đường tròn (A, B là tiếp điểm). Vẽ đường tròn (O') đi qua C và tiếp xúc với AB tại B, cắt (O) ở M. CMR đường thẳng AM đi qua TĐ của BC.

Những câu hỏi liên quan
Cho đường tròn (O) và điểm C nằm nên ngoài đường tròn. Qua C kẻ tiếp tuyên CA, CB với đường tròn (A, B là tiếp điểm). Vẽ đường tròn (O') đi qua C và tiếp xúc với AB tại B, cắt (O) ở M. CMR đường thẳng AM đi qua TĐ của BC.
Cho đường tròn (O), từ điểm m ngoài đường tròn kẻ 2 tiếp tuyến MA và MB. Đường tròn đi qua M tiếp xúc Với AB tại B cắt đường tròn (O) tại C. Chứng mình CA đi qua trung điểm MB
Cho (O;R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ tiếp tuyến AB tiếp xúc với đường tròn (O) tại B. Vẽ một đường thẳng qua A cắt đường tròn tại hai điểm M và N ( M nằm giữa A và N). Qua M kẻ đường thẳng song song với AB cắt BN tại E. Gọi I là trung điểm của ME. Vẽ dây BQ của đường tròn (O) sao cho BQ đi qua điểm Ia) Chứng minh hai tam giác BMI và tam giác BQM đồng dạngb)Chứng minh tứ giác QIEN nội tiếpc) Chứng minh BM.QNBN.MQ
Đọc tiếp
Cho (O;R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ tiếp tuyến AB tiếp xúc với đường tròn (O) tại B. Vẽ một đường thẳng qua A cắt đường tròn tại hai điểm M và N ( M nằm giữa A và N). Qua M kẻ đường thẳng song song với AB cắt BN tại E. Gọi I là trung điểm của ME. Vẽ dây BQ của đường tròn (O) sao cho BQ đi qua điểm I
a) Chứng minh hai tam giác BMI và tam giác BQM đồng dạng
b)Chứng minh tứ giác QIEN nội tiếp
c) Chứng minh BM.QN=BN.MQ
Cho đường tròn (O;R) và một điểm A nằm ngoài đường tròn. Kẻ một đường thẳng qua A và không đi qua tâm O, cắt đường tròn tại 2 điểm phân biệt M, N (M nằm giữa A và N). Từ A vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là hai tiếp điểm). Đường thẳng BC cắt AO tại H. Gọi I là trung điểm của MN.a) Chứng minh tứ giác ACOI là tứ giác nội tiếp.b) Chứng minh OI.OE OH.OA AC2.c) Tính theo R độ dài của OA biết diện tích của tứ giác ABOC bằng 3R2.b bic làm bài này hok zgiúp mik vs ạ
Đọc tiếp
Cho đường tròn (O;R) và một điểm A nằm ngoài đường tròn. Kẻ một đường thẳng qua A và không đi qua tâm O, cắt đường tròn tại 2 điểm phân biệt M, N (M nằm giữa A và N). Từ A vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là hai tiếp điểm). Đường thẳng BC cắt AO tại H. Gọi I là trung điểm của MN.
a) Chứng minh tứ giác ACOI là tứ giác nội tiếp.
b) Chứng minh OI.OE = OH.OA = AC2.
c) Tính theo R độ dài của OA biết diện tích của tứ giác ABOC bằng 3R2.
b bic làm bài này hok z
giúp mik vs ạ
Cho điểm A nằm bên ngoài đường tròn (O). Qua A, kẻ hai tiếp tuyến tiếp xúc đường tròn (O) tại B và C. Gọi M là điểm di động luôn nằm giữa A và C. Qua M, kẻ tiếp tuyến thứ hai tiếp xúc đường tròn (O) tại I (I khác C). Tia MI cắt đoạn thẳng AB tại N.a) Khi M di động, chứng tỏ tam giác AMN có chu vi không đổi.b) Qua O, kẻ đường thẳng vuông góc với OA; đường thẳng vừa kẻ lần lượt cắt các tia AC, AB tại P và Q. Chứng minh OP OQ.c) Chứng minh tam giác POM đồng dạng với tam giác QNO.d) chứng minh tổng...
Đọc tiếp
Cho điểm A nằm bên ngoài đường tròn (O). Qua A, kẻ hai tiếp tuyến tiếp xúc đường tròn (O) tại B và C. Gọi M là điểm di động luôn nằm giữa A và C. Qua M, kẻ tiếp tuyến thứ hai tiếp xúc đường tròn (O) tại I (I khác C). Tia MI cắt đoạn thẳng AB tại N.
a) Khi M di động, chứng tỏ tam giác AMN có chu vi không đổi.
b) Qua O, kẻ đường thẳng vuông góc với OA; đường thẳng vừa kẻ lần lượt cắt các tia AC, AB tại P và Q. Chứng minh OP = OQ.
c) Chứng minh tam giác POM đồng dạng với tam giác QNO.
d) chứng minh tổng PM + QN lớn hơn hoặc bằng PQ.
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ đường tròn (7) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại Da, Nêu cách vẽ đường tròn (I) nói trênb, Đường tròn (I) cắt cắt CA, CB lần lượt tại các điểm thứ hai là M, N. Chứng minh M, I, N thẳng hàngc, Chứng minh đường thẳng CD đi qua điểm chính giữa nửa đường tròn (O) không chứa C
Đọc tiếp
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ đường tròn (7) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại D
a, Nêu cách vẽ đường tròn (I) nói trên
b, Đường tròn (I) cắt cắt CA, CB lần lượt tại các điểm thứ hai là M, N. Chứng minh M, I, N thẳng hàng
c, Chứng minh đường thẳng CD đi qua điểm chính giữa nửa đường tròn (O) không chứa C
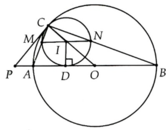
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm
Đúng 0
Bình luận (0)
Từ điểm A nằm ngoài đường tròn (O) kẻ tiếp tuyến AM với đường tròn (M là tiếp điểm). Kẻ dây MN vuông góc với AO tại H. Kẻ đường thẳng đi qua A cắt đường tròn tại B,C(điểm B nằm giữa A và C). Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại K, gọi I là trung điểm của BC.
a) Chứng minh 4 điểm B,C,O,K cùng thuộc một đường tròn.
b) Chứng minh AN là tiếp tuyến của đường tròn (O)
c) Chứng minh OI.OKON²
d) Chứng minh M,N,K thẳng hàng.
Đọc tiếp
Từ điểm A nằm ngoài đường tròn (O) kẻ tiếp tuyến AM với đường tròn (M là tiếp điểm). Kẻ dây MN vuông góc với AO tại H. Kẻ đường thẳng đi qua A cắt đường tròn tại B,C(điểm B nằm giữa A và C). Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại K, gọi I là trung điểm của BC. a) Chứng minh 4 điểm B,C,O,K cùng thuộc một đường tròn. b) Chứng minh AN là tiếp tuyến của đường tròn (O) c) Chứng minh OI.OK=ON² d) Chứng minh M,N,K thẳng hàng.
a: Xét tứ giác OBKC có \(\widehat{OBK}+\widehat{OCK}=90^0+90^0=180^0\)
nên OBKC là tứ giác nội tiếp
=>O,B,K,C cùng thuộc một đường tròn
b: Ta có: ΔOMN cân tại O
mà OA là đường cao
nên OA là phân giác của góc MON
Xét ΔMOA và ΔNOA có
OM=ON
\(\widehat{MOA}=\widehat{NOA}\)
OA chung
Do đó: ΔMOA=ΔNOA
=>\(\widehat{OMA}=\widehat{ONA}\)
=>\(\widehat{ONA}=90^0\)
=>AN là tiếp tuyến của (O)
c: Xét (O) có
KB,KC là tiếp tuyến
Do đó: KB=KC
=>K nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OK là đường trung trực của BC
=>OK\(\perp\)BC tại I và I là trung điểm của BC
Xét ΔOBK vuông tại B có BI là đường cao
nên \(OI\cdot OK=OB^2\)
=>\(OI\cdot OK=ON^2\left(3\right)\)
d: Xét ΔNOA vuông tại N có NH là đường cao
nên \(OH\cdot OA=ON^2\left(4\right)\)
Từ (3) và (4) suy ra \(OI\cdot OK=OH\cdot OA\)
=>\(\dfrac{OI}{OH}=\dfrac{OA}{OK}\)
Xét ΔOIA và ΔOHK có
\(\dfrac{OI}{OH}=\dfrac{OA}{OK}\)
\(\widehat{HOK}\) chung
Do đó: ΔOIA đồng dạng với ΔOHK
=>\(\widehat{OIA}=\widehat{OHK}\)
=>\(\widehat{OHK}=90^0\)
mà \(\widehat{OHM}=90^0\)
nên K,H,M thẳng hàng
mà M,H,N thẳng hàng
nên K,M,N thẳng hàng
Đúng 0
Bình luận (0)
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn . Qua M vẽ hai tiếp tuyến MA , MB với đường tròn (O) trong đó A , B là hai tiếp điểm sao cho AMB = 90 độ . Qua điểm C trên cung nhỏ AB kẻ tiếp tuyến với đường tròn (o) cắt MA , MB tại P vs Q .
CMR : 1/3 ( MA + MB ) < PQ < 1/2 ( MA + MB)
o l m . v n
một điểm A nằm ngoài đường tròn (O;R) kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B vuông góc với OA tại H và cắt đường trong (O) tại C. Vẽ đường kính BD. Đường thẳng AO cắt đường tròn (O) tại 2 điểm M và N (M nằm giữa A và N). Chứng minh:a) CD//OAb) AC là tiếp tuyến của đường tròn (O)c) Cho biết R 15cm, BC 24CM. Tính AB, OAd) Gọi I là trung điểm của HN. Từ H kẻ đường vuông góc với BI cắt BM tại E. Chứng minh: M là trung điểm của BE.
Đọc tiếp
một điểm A nằm ngoài đường tròn (O;R) kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B vuông góc với OA tại H và cắt đường trong (O) tại C. Vẽ đường kính BD. Đường thẳng AO cắt đường tròn (O) tại 2 điểm M và N (M nằm giữa A và N). Chứng minh:a) CD//OAb) AC là tiếp tuyến của đường tròn (O)c) Cho biết R = 15cm, BC = 24CM. Tính AB, OAd) Gọi I là trung điểm của HN. Từ H kẻ đường vuông góc với BI cắt BM tại E. Chứng minh: M là trung điểm của BE.













