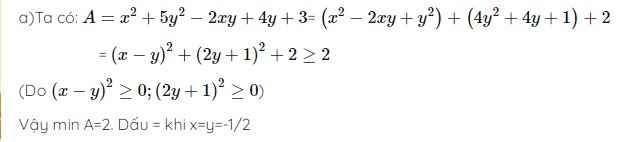tìm GTLN của biểu thức B= -2x2+5x-8

Những câu hỏi liên quan
Tìm GTLN của các biểu thức sau:
A = 6x - 3x2 - 7
B = 5x - 2x2 + 1
C = 2x2 - 8x + 13
D = x2 - 3x + 5
\(A=-3x^2+6x-7=-3\left(x^2-2x+1-1\right)-7\)
\(=-3\left(x-1\right)^2-4\le-4\)Dấu ''='' xảy ra khi x = 1
\(B=-2x^2+5x+1=-2\left(x^2-\dfrac{5}{2}x\right)+1\)
\(=-2\left(x^2-2.\dfrac{5}{4}x+\dfrac{25}{16}-\dfrac{25}{16}\right)+1\)
\(=-2\left(x-\dfrac{5}{4}\right)^2+\dfrac{33}{8}\le\dfrac{33}{8}\)Dấu ''='' xảy ra khi x = 5/4
C;D chỉ có GTNN thôi bạn nhé \(C=2x^2-8x+13=2\left(x^2-4x+4-4\right)+13\)
\(=2\left(x-2\right)^2+5\ge5\)Dấu ''='' xảy ra khi x = 2
\(D=x^2-3x+5=x^2-2.\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}+5\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\)Dấu ''='' xảy ra khi x = 3/2
Đúng 2
Bình luận (0)
d: Ta có: \(D=x^2-3x+5\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{11}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm GTNN hoặc GTLN của các biểu thức sau:
a) A = x2 + 3x + 4
b) B = 2x2 - x + 1
c) C = 5x - x2 + 4
d) D = x2 + 5y2 - 2xy + 4y + 3
a: Ta có: \(A=x^2+3x+4\)
\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\)
\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Tìm GTNN hoặc GTLN của các biểu thức sau:
a) 2x2 - x + 1
b) 5x - x2 + 4
c) x2 + 5y2 - 2xy + 4y + 3
a) \(2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{4}\)
b) \(5x-x^2+4=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\)
\(ĐTXR\Leftrightarrow x=\dfrac{5}{2}\)
c) \(x^2+5y^2-2xy+4y+3=\left(x-y\right)^2+\left(2y+1\right)^2+2\ge2\)
\(ĐTXR\Leftrightarrow\)\(x=y=-\dfrac{1}{2}\)
Đúng 3
Bình luận (0)
b: ta có: \(-x^2+5x+4\)
\(=-\left(x^2-5x-4\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{41}{4}\right)\)
\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
cho biểu thức P=2x-2xy-2x2-y2.Tìm GTLN của biểu thức P, khi P= GTLN thì x, y bằng mấy
Ta có: \(P=2x-2xy-2x^2-y^2\)
\(P=-x^2-2xy-y^2-x^2+2x\)
\(P=-\left(x^2+2xy+y^2\right)-\left(x^2-2x+1\right)+1\)
\(P=-\left(x+y\right)^2-\left(x-1\right)^2+1\)
\(P=-\left[\left(x+y\right)^2+\left(x-1\right)^2\right]+1\le1\forall x;y\)
Vậy GTLN của P là 1 khi x=-1; y=1.
Đúng 0
Bình luận (0)
Cho biểu thức
C
x
+
2
x
2
-
5
x
+
x
-
2
x
2
+
5...
Đọc tiếp
Cho biểu thức C = x + 2 x 2 - 5 x + x - 2 x 2 + 5 x : x 2 + 10 x 2 - 25
b) Tìm x để giá trị của biểu thức C bằng 2.
b) Vậy C = 2 ⇒ (2/x) = 2
⇒ x = 1(thỏa mãn các điều kiện trên).
Đúng 0
Bình luận (0)
Cho biểu thức
5
x
+
2
x
2
-
10
x
+
5
x
-
2
x
2
+...
Đọc tiếp
Cho biểu thức 5 x + 2 x 2 - 10 x + 5 x - 2 x 2 + 10 x . x 2 - 100 x 2 + 4 . Tìm điều kiện của x để giá trị của biểu thức được xác định
Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
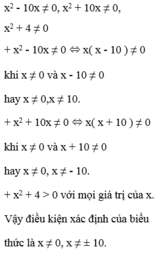
Đúng 0
Bình luận (0)
Cho biểu thức
5
x
+
2
x
2
-
10
x
+
5
x
-
2
x
2
+...
Đọc tiếp
Cho biểu thức 5 x + 2 x 2 - 10 x + 5 x - 2 x 2 + 10 x . x 2 - 100 x 2 + 4 . Tìm điều kiện của x để giá trị của biểu thức được xác định.
Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:

Đúng 0
Bình luận (0)
tìm GTNN của biểu thức A= 2x2-8x+1
Tìm GTLN của B = -5x2-4x+1
cảm ơn nha^^
a: Ta có: \(A=2x^2-8x+1\)
\(=2\left(x^2-4x+\dfrac{1}{2}\right)\)
\(=2\left(x^2-4x+4-\dfrac{7}{2}\right)\)
\(=2\left(x-2\right)^2-7\ge-7\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 2
Bình luận (0)
Tìm GTLN, GTNN của biểu thức chứa dấu GTTĐ.
1-2|2-2x2|
|2-2x^2|>=0
=>-2|2x^2-2|<=0
=>-2|2x^2-2|+1<=1
Dấu = xảy ra khi 2x^2-2=0
=>x^2=1
=>x=1 hoặc x=-1
Đúng 1
Bình luận (0)