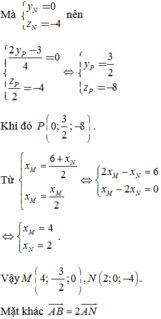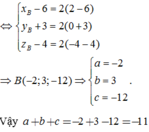C(2,2,-1) oxy oxz, oyz

Những câu hỏi liên quan
Tìm toạ độ điểm H là hình chiếu của M lên đường thẳng hoặc mặt phẳng có M(-3,7,-4) lên (Oxy),(Oxz),(Oyz)
Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm
M
1
;
3
;
2
đến ba mặt phẳng tọa độ
O
x
y
,
O
y
z
,
O
x
z
. Tính ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm M 1 ; 3 ; 2 đến ba mặt phẳng tọa độ O x y , O y z , O x z . Tính P = a + b 2 + c 3
A. P = 12.
B. P = 32.
C. P = 30.
D. P = 18.
Đáp án C
Áp dụng STUDY TIPS bên, ta có:
Khoảng cách từ điểm M đến mặt phẳng O x y là a=2.
Khoảng cách từ điểm M đến mặt phẳng O x y là b=1.
Khoảng cách từ điểm M đến mặt phẳng O x y là c=3 .
Vậy P = a + b 2 + c 3 = 2 + 1 2 + 3 3 = 30 .
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm M(1;3;2) đến ba mặt phẳng tọa độ (Oxy), (Oyz), (Oxz). Tính P = a + b 2 + c 3
A. 12
B. 32
C. 30
D. 18
Trong không gian với hệ tọa độ Oxyz, gọi a,b,c lần lượt là khoảng cách từ điểm M(1;3;2) đến ba mặt phẳng tọa độ (Oxy), (Oyz), (Oxz). Tính P = a + b 2 + c 3
A. 12
B. 32
C. 30
D. 18
Gọi A1,A2,A3 lần lượt là hình chiếu vuông góc của A=(-1;2;3) lên các mặt phẳng (oxy),(oxz),(oyz) phương trình mặt phẳng(A1A2A3) là?
Gọi A1,A2,A3 lần lượt là hình chiếu vuông góc của A=(-1;2;3) lên các mặt phẳng (oxy),(oxz),(oyz) phương trình mặt phẳng(A1A2A3) là?
Gọi A1,A2,A3 lần lượt là hình chiếu vuông góc của A=(-1;2;3) lên các mặt phẳng (oxy),(oxz),(oyz) phương trình mặt phẳng(A1A2A3) là?
Lời giải:
Vì \(A_1,A_2,A_3 \) là hình chiếu của \(A\) lên các mặt phẳng tọa độ nên :
\(\left\{\begin{matrix} A_1=(-1,2,0)\\ A_2=(-1,0,3)\\ A_3=(0,2,3)\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \overrightarrow {A_1A_2}=(0,-2,3)\\ \overrightarrow {A_1A_3}=(1,0,3)\\ \end{matrix}\right.\)
Vector pháp tuyến của \((A_1A_2A_3):\overrightarrow{n_P}=[\overrightarrow {A_1A_2},\overrightarrow {A_1A_3}]=(-6,3,2)\)
Suy ra PTMP:
\(-6(x-0)+3(y-2)+2(z-3)=0\Leftrightarrow -6x+3y+2z-12=0\)
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M thỏa mãn OM 7. Biết rằng khoảng cách từ M đến (Oxz), (Oyz) lần lượt là 2 và 3. Tính khoảng cách từ M đến (Oxy). A. 12 B. 5 C. 2 D. 6
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M thỏa mãn OM = 7. Biết rằng khoảng cách từ M đến (Oxz), (Oyz) lần lượt là 2 và 3. Tính khoảng cách từ M đến (Oxy).
A. 12
B. 5
C. 2
D. 6
Đáp án D
Gọi M ( a ; b ; c ) ⇒ d M , O x z = b = 2 ; d M , O y z = a = 3
Do O M = 7 ⇒ a 2 + b 2 + c 2 = 49 ⇒ c = 49 - a 2 - b 2 = 6
Vậy d M ; O x y = 6 .
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai điểm
A
6
;
−
3
;
4
,
B
a
;
b
;
c
. Gọi M, N, P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ (Oxy), (Oxz), (Oyz). Biết rằng M, N, P nằm trên đoạn AB sao cho AM MN NP PB. Tính giá trị của...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A 6 ; − 3 ; 4 , B a ; b ; c . Gọi M, N, P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ (Oxy), (Oxz), (Oyz). Biết rằng M, N, P nằm trên đoạn AB sao cho AM = MN = NP = PB. Tính giá trị của tổng a + b + c
A. 11
B. -11
C. 17
D. -17
Trong không gian Oxyz, cho hai điểm
A
6
;
−
3
;
4
,
B
a
;
b
;
c
. Gọi M, N, P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ (Oxy), (Oxz), (Oyz). Biết rằng M, N, P nằm trên đoạn AB sao cho AM MN NP PB. Tính giá trị của...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A 6 ; − 3 ; 4 , B a ; b ; c . Gọi M, N, P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ (Oxy), (Oxz), (Oyz). Biết rằng M, N, P nằm trên đoạn AB sao cho AM = MN = NP = PB. Tính giá trị của tổng a + b + c.
A. a+b+c = 11
B.a+b+c = -11
C.a+b+c = 17
D.a+b+c = -17
Đáp án B.
Các phương trình O x y : z = 0 ; O x y : x = 0 ; O x y : y = 0 . Giả sử M x M ; y M ; 0 , N x N ; 0 ; z N , P 0 ; y p ; z p . Tính theo giả thiết có M là trung điểm của AN nên ta có M 6 + x N 2 ; − 3 2 ; 4 + z N 2 . Do z M = 0 nên 4 + z N 2 = 0 ⇔ z N = − 4 ⇒ M x M ; − 3 2 ; 0 và N x N ; 0 ; − 4 .
Lại có N là trung điểm của MP nên N x M 2 ; 2 y P − 3 4 ; z P 2 .
Mà y N = 0 z N = − 4 nên 2 y P − 3 4 = 0 z P 2 = − 4 ⇔ y P = 3 2 z P = − 8 Khi đó P 0 ; 3 2 ; − 8 .
Từ
x M = 6 + x N 2 x M = x M 2 ⇔ 2 x M − x N = 6 x M − 2 x N = 0 ⇔ x M = 4 x N = 2
Vậy M 4 ; − 3 2 ; 0 , N 2 ; 0 ; − 4 .
Mặt khác
A B → = 2 A N → ⇔ x B − 6 = 2 ( 2 − 6 ) y B + 3 = 2 ( 0 + 3 ) z B − 4 = 2 ( − 4 − 4 ) ⇒ B ( − 2 ; 3 ; − 12 ) ⇒ a = − 2 b = 3 c = − 12 .
Vậy a + b + c = − 2 + 3 − 12 = − 11
Đúng 0
Bình luận (0)