ĐKXĐ: \(x\ne0\)

phân thức xác định khi
\(x^2+x-2\ne0\)
\(x^2+2x-x-2\ne0\)
\(x\left(x+2\right)-\left(x+2\right)\ne0\)
\(\left(x-1\right)\left(x+2\right)\ne0\)
\(x-1\ne0vàx+2\ne0\)
\(x\ne1\) và \(x\ne-2\)

ĐKXĐ: \(x\notin\left\{-2;1\right\}\)

\(a,\dfrac{x^3-2^3}{x^2-4}=\dfrac{\left(x-2\right)\left(x^2-2x+4\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2-2x+4}{x+2}\\ b,\dfrac{2}{2x-4}=\dfrac{2}{2\left(x-2\right)}=\dfrac{1}{x-2}\\ \dfrac{3}{3x-6}=\dfrac{3}{3\left(x-2\right)}=\dfrac{1}{x-2}\)

a: \(\dfrac{x^2-4x+4}{x^2-2x}=\dfrac{\left(x-2\right)^2}{x\left(x-2\right)}=\dfrac{x-2}{x}=\dfrac{\left(x-2\right)\left(x-1\right)}{x\left(x-1\right)}\)

\(\dfrac{x+1}{x^2-1}=\dfrac{1}{x-1}=\dfrac{x}{x\left(x-1\right)}\)

b: \(\dfrac{x^3-2^3}{x^2-4}=\dfrac{x^2+2x+4}{x+2}\)

3/x+2=3/x+2

\(\dfrac{x}{4+2a}\) có nghĩa khi \(a\ne-2\)

\(\dfrac{y}{4-2a}\)có nghĩa khi \(a\ne2\)

\(\dfrac{z}{4-a^2}\)có nghĩa khi \(a\ne\pm2\)

MTC: \(2\left(2+a\right)\left(2-a\right)\)

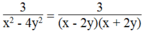 xác định khi:

(x – 2y)(x + 2y) ≠ 0 ⇔ 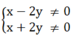 ⇒ x  ≠   ± 2y

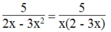xác định khi:

x(2 – 3x) ≠ 0 ⇔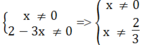 

Vậy phân thức  5 2 x - 3 x 2  xác định với x ≠ 0 và x ≠ 2/3

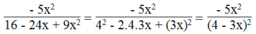 xác định khi:

4 - 3 x 2 ≠ 0 ⇒ 4 – 3x  ≠  0 ⇒ x  ≠  4/3

 xác định khi 2 x + 1 3 ≠ 0

Suy ra: 2x + 1 ≠ 0 ⇒ x  ≠  - 1/2

\(\dfrac{x^3-x^2-x+1}{x^4-2x^2+1}=\dfrac{x^2\left(x-1\right)-\left(x-1\right)}{\left(x-1\right)^2\cdot\left(x+1\right)^2}=\dfrac{\left(x-1\right)^2\cdot\left(x+1\right)}{\left(x-1\right)^2\cdot\left(x+1\right)^2}=\dfrac{1}{x+1}\)

\(\dfrac{5x^3+10x^2+5x}{x^3+3x^2+3x+1}=\dfrac{5x\left(x+1\right)^2}{\left(x+1\right)^3}=\dfrac{5x}{x+1}\)