Cho hình thoi ABCD có góc A = 60 độ. Gọi O là giao điểm của 2 đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Chứng minh rằng sáu điểm E, B, F, G, D, H thuộc cùng 1 đường tròn
Những câu hỏi liên quan
Cho hình thoi ABCD cạnh a có BAD=60 độ. Gọi O là giao điểm của hai đường chéo AC và BD. Gọi O là giao điểm hai đường chéo AC và BD. Gọi G là trọng tâm tam giác ABD, E là điểm đối xứng của O qua D, H là giao điểm AD và GE. Tính độ dài vector AH
cho hình thoi ABCD có góc A=60 độ, gọi P là trung điểm của AB, N là giao điểm của đường thẳng AD và CD. CMR:
a) diện tích hình thoi = 4diện tích tam giác PBC
b) gọi N là giao điểm của BN và DP. CM: PA.PB=PD.PM
Bài 13: Cho hình thoi ABCD, biết O là giao điểm của hai đường chéo và góc BAO40 độ
a) Tính góc BAD
b) Tính các góc còn lại của hình thoi.
Đọc tiếp
Bài 13: Cho hình thoi ABCD, biết O là giao điểm của hai đường chéo và góc BAO=40 độ
a) Tính góc BAD
b) Tính các góc còn lại của hình thoi.
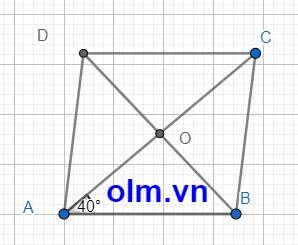
Vì ABCD là hình thoi nên ⇒ tam giác ABD cân tại A
Vì O là trung điểm DB nên AO là truyến là đường phân giác của tam giác ABD
⇒ \(\widehat{DAO}\) = 400
⇒ \(\widehat{DAB}\) = 400 + 400 = 1800
⇒ \(\widehat{ADC}\) = 1800 - 800 = 1000
⇒ \(\widehat{DCB}\) = 1800 - 1000 = 800
\(\Rightarrow\) \(\widehat{ABC}\) = 1800 - 800 = 1000
Đúng 1
Bình luận (0)
cho hình thoi ABCD gọi o là giao điểm hai đường chéo biết AB = 20 cm OA = 16 cm OB = 12 cm tính độ dài các cạnh và đường chéo của hình thoi
Vì ABCD là hình thoi nên \(AB=BC=CD=DA=20\left(cm\right)\)
Và AC cắt BD tại O nên O là trung điểm AC,BD
\(\Rightarrow AC=2AO=32\left(cm\right);BD=2OB=24\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình thoi ABCD .Gọi O là giao điểm của AC và BD.Gọi E,F là hình chiếu của O trên BC,CD.Tính các góc của hình thoi biết rằng EF=1/4 đường chéo hình thoi
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a,
A
D
C
^
60
∘
. Gọi O là giao điểm của AC và BD, SO vuông góc với (ABCD) và SOa. Góc giữa đường thẳng SD và (ABCD) bằng A.
60
∘
B.
75
∘
C.
30
∘
D.
45...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, A D C ^ = 60 ∘ . Gọi O là giao điểm của AC và BD, SO vuông góc với (ABCD) và SO=a. Góc giữa đường thẳng SD và (ABCD) bằng
A. 60 ∘
B. 75 ∘
C. 30 ∘
D. 45 ∘
cho hình thoi abcd có góc b bằng 60 độ, O là giao điểm của 2 đường chéo. trên BC laaysddieemr M sao cho BM=4/3BC, N là giao của AM và CD. trên AB, AD lấy E, F theo thứ tự sao cho CE//NF
a, CM BE.DF = BO^2
b, tính góc EOF
Cho hình thoi ABCD, độ dài mỗi cạnh là 13cm. Gọi O là giao điểm hai đường chéo. Vẽ OH vuông góc AD. Biết OH=6cm, tính tỉ số hai đường chéo BD và AC
Cho hình thoi ABCD có ∠ A = 60 ° . Gọi O là giao điểm của hai đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Chứng minh rằng sáu điểm E, B, F, G, D, H thuộc cùng một đường tròn.
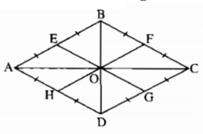
Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O;a).
Đúng 0
Bình luận (0)