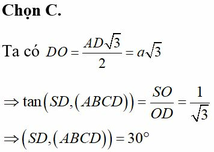Các câu hỏi tương tự
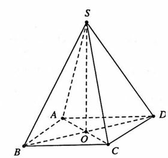
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và góc
S
D
;
A
B
C
D
^
60
°
. Gọi a là góc giữa...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và góc S D ; A B C D ^ = 60 ° . Gọi a là góc giữa hai mặt phẳng (SCD) và (ABCD). Tính tanα
A. tan α = 4 15 9
B. tan α = 30 12
C. tan α = 10 3
D. tan α = 30 3
Cho hình chóp
S
.
A
B
C
D
có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng
A
B
C
D
là trung điểm H của đoạn OA và
S
D
,
A
B
C...
Đọc tiếp
Cho hình chóp S . A B C D có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng A B C D là trung điểm H của đoạn OA và S D , A B C D = 60 ∘ . Gọi α là góc giữa hai mặt phẳng S C D v à A B C D . Tính t a n α .
A. t a n α = 4 15 9
B. tan α = 30 12
C. tan α = 10 3
D. tan α = 30 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc
A
B
C
^
60
∘
cạnh bên
S
D
a
2
. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho
H
D
→
-
3
H...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc A B C ^ = 60 ∘ cạnh bên S D = a 2 . Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho H D → = - 3 H B → . Gọi M là trung điểm của cạnh SD. Tính khoảng cách giữa hai đường thẳng CM và SB.
A. a 30 8
B. a 7 4
C. 30 a 7
D. a 30 17
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a,
A
D
a
3
, SA vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng
60
°
. Gọi M là trung điểm của cạnh AD. Khoảng cách giữa hai đường thẳng CM và SB bằng A.
6
a
22
11
B.
3
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, A D = a 3 , SA vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AD. Khoảng cách giữa hai đường thẳng CM và SB bằng
A. 6 a 22 11
B. 3 a 22 11
C. a 3
D. a 7 2
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và tma giác ABD đều. SO vuông góc mặt phẳng (ABCD) và SO2a. M là trung điểm của SD. Tang góc giữa CM và (ABCD) là: A.
4
13
B.
4
13
13
C.
13
4
D.
13
13
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và tma giác ABD đều. SO vuông góc mặt phẳng (ABCD) và SO=2a. M là trung điểm của SD. Tang góc giữa CM và (ABCD) là:
A. 4 13
B. 4 13 13
C. 13 4
D. 13 13
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
°
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC A.
a
5
5
B.
5
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 3
D. 2 a 5 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
°
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD)nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC A.
a
5
5
B.
5
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD)nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 5
D. 2 a 5 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và
S
D
,
A
B
C
D
^
60
0
. Gọi...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và S D , A B C D ^ = 60 0 . Gọi α là góc giữa hai mặt phẳng (SCD) và (ABCD). Tính tan α .
A. tan α = 4 15 9 .
B. tan α = 30 12 .
C. tan α = 10 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM) A.
d
3
a
2
.
B.
d
a
.
C.
d
2
a
3
.
D. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA=2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM)
A. d = 3 a 2 .
B. d = a .
C. d = 2 a 3 .
D. d = a 3 .