ab=5cm.Vẽ đường thẳng bc đi qua điểm b vương góc với ab

Những câu hỏi liên quan
Cho tam giác đều ABC , E là điểm thuộc AC, K là điểm thuộc AE. Đường thẳng È đi qua E vương góc với AB cắt đường thẳng qua C vuông góc với BC taiD
a)tu giac BCKf la hinh gi
b)cung minh KE.EC=ED.EF
cho tam giác abc vuông tại a, i là trung điểm của ab, đường thẳng qua i và vuông góc với bc cắt đường thẳng đi qua b vuông góc với ab ở d. cmr: ad vuông góc id.
Xem chi tiết
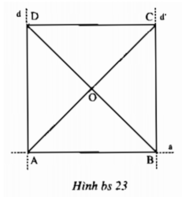
Vẽ hình theo diễn đạt:Vẽ đường thẳng a . Trên đường thẳng a vẽ đoạn thẳng AB 4 (cm) . Vẽ đường thẳng d đi qua điểm A và vuông góc với a . Vẽ đường thẳng d đi qua điểm B và vuông góc với .Trên đường thẳng d lấy điểm D sao cho AD AB . Trên đường thẳng d lấy điểm C sao cho hai điểm C , D nằm về cùng phía với đường thẳng a và BC AB . Vẽ các đoạn thẳng CD , AC , BD . Gọi O là giao điểm của AB và CD
Đọc tiếp
Vẽ hình theo diễn đạt:
Vẽ đường thẳng a . Trên đường thẳng a vẽ đoạn thẳng AB = 4 (cm) . Vẽ đường thẳng d đi qua điểm A và vuông góc với a . Vẽ đường thẳng d' đi qua điểm B và vuông góc với .Trên đường thẳng d lấy điểm D sao cho AD = AB . Trên đường thẳng d' lấy điểm C sao cho hai điểm C , D nằm về cùng phía với đường thẳng a và BC = AB . Vẽ các đoạn thẳng CD , AC , BD . Gọi O là giao điểm của AB và CD
Đường trung trực của đoạn thẳng AB là:
A. Đường thẳng đi qua trung điểm AB.
B. Đường thẳng vuông góc với AB.
C. Đường thẳng vuông góc với AB tại trung điểm đoạn thẳng AB.
D. Đường thẳng vuông góc với AB tại một điểm bất kì trên AB
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.
Giả sử ΔABC đều có cạnh bằng a, kẻ đường cao AD, đặt AD = h không đổi.
Ta có:
S A B C = 1/2 ah
S M A B = 1/2 MT.a
S M A C = 1/2 MK.a
S M B C = 1/2 MH.a
S A B C = S M A B + S M A C + S M B C
1/2 a.h = 1/2 MT.a + 1/2 MK.a + 1/2 MH.a
1/2 a. (MT + MK + MH)
⇒ MT + MK + MH = h không đổi
Vậy tổng MT + MK + MH không phụ thuộc vào điểm M.
Đúng 0
Bình luận (0)
Vẽ đường thẳng a. Trên đường thẳng a vẽ đoạn thẳng AB 4 (cm). Vẽ đường thẳng d đi qua điểm A và vuông góc với a. Vẽ đường thẳng d’ đi qua điểm B và vuông góc với a. Trên đường thẳng d lấy điểm D sao cho AD AB. Trên đường thẳng d’ lấy điểm C sao cho hai điểm C, D nằm về cùng phía với đường thẳng a và BC AB. Vẽ các đoạn thẳng CD, AC, BD. Gọi O là giao điểm của AC và BD.a) Đo và cho biết số đo góc ADC.b) Đo và cho biết số đo góc BCD.C) Đo và cho biết số đo góc BOC
Đọc tiếp
Vẽ đường thẳng a. Trên đường thẳng a vẽ đoạn thẳng AB = 4 (cm). Vẽ đường thẳng d đi qua điểm A và vuông góc với a. Vẽ đường thẳng d’ đi qua điểm B và vuông góc với a. Trên đường thẳng d lấy điểm D sao cho AD = AB. Trên đường thẳng d’ lấy điểm C sao cho hai điểm C, D nằm về cùng phía với đường thẳng a và BC = AB. Vẽ các đoạn thẳng CD, AC, BD. Gọi O là giao điểm của AC và BD.
a) Đo và cho biết số đo góc ADC.
b) Đo và cho biết số đo góc BCD.
C) Đo và cho biết số đo góc BOC
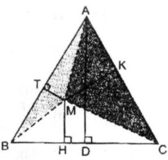
Cho tam giác nhọn ABC có ABAC, các đường cao AD, BE, CF cắt nhau tại H. ĐƯờng thẳng đi qua C và vuông góc với AC cắt đường thẳng đi qua B và vuông góc với AB tại điểm K. Gọi M là trung điểm của BC, I là trung điểm của AKa) CHứng minh: BECF và IMdfrac{1}{2}AHb) Gọi G là trọng tâm của tam giác ABC. CHứng minh: 3 điểm H, G, I thẳng hàng. c) CM: dfrac{HD}{AD}+dfrac{HE}{BE}+dfrac{HF}{CF}1
Đọc tiếp
Cho tam giác nhọn ABC có AB<AC, các đường cao AD, BE, CF cắt nhau tại H. ĐƯờng thẳng đi qua C và vuông góc với AC cắt đường thẳng đi qua B và vuông góc với AB tại điểm K. Gọi M là trung điểm của BC, I là trung điểm của AK
a) CHứng minh: BE<CF và \(IM=\dfrac{1}{2}AH\)
b) Gọi G là trọng tâm của tam giác ABC. CHứng minh: 3 điểm H, G, I thẳng hàng.
c) CM: \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\)
a) Ta có:
\(\left\{{}\begin{matrix}BH\perp AC\\KC\perp AC\end{matrix}\right.\) ⇒ \(BH\text{//}KC\)
\(\left\{{}\begin{matrix}CH\perp AB\\BK\perp AB\end{matrix}\right.\) ⇒ \(CH\text{//}BK\)
\(Xét\) \(tứ\) \(giác\) \(BKCH\) \(có:\) \(\left\{{}\begin{matrix}BH\text{//}KC\\CH\text{//}BK\end{matrix}\right.\)
⇒ Tứ giác \(BKCH\) là hình hình hành. Mà M là trung điểm của đường chéo BC
⇒ \(\left\{{}\begin{matrix}H,M,K_{ }thẳng_{ }hàng\\HM=MK\end{matrix}\right.\)
Xét \(\Delta AHK\) có: \(\left\{{}\begin{matrix}AI=IK\left(gt\right)\\HM=MK\left(cmt\right)\end{matrix}\right.\)
⇒ \(IM\) là đường trung bình của \(\Delta AHK\)
⇒ \(IM=\dfrac{1}{2}AH\) \(\left(ĐPCM\right)\)
c)
Ta có:
\(\dfrac{S_{\Delta HBC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HD.BC}{\dfrac{1}{2}.AD.BC}=\dfrac{HD}{AD}\)
\(\dfrac{S_{\Delta HAC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HE.AC}{\dfrac{1}{2}.BE.AC}=\dfrac{HE}{BE}\)
\(\dfrac{S_{\Delta HBA}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HF.AB}{\dfrac{1}{2}.CF.AB}=\dfrac{HF}{CF}\)
⇒ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{\Delta HBC}+S_{\Delta HAC}+S_{\Delta HAB}}{S_{\Delta ABC}}=\dfrac{S_{\Delta ABC}}{S_{\Delta ABC}}\)
⇔ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\) \(\left(ĐPCM\right)\)
Đúng 3
Bình luận (0)
Cho tứ giác ABCD . Gọi M , N lần lượt là trung điểm AB ,AD. CMR: đường thẳng đi qua điểm M vuông góc với CD, đường thẳng đi qua điểm N vuông góc với BC và đường thẳng AC đồng quy với nhau
a) Vẽ đường thẳng AB và điểm H không nằm trên đường thẳng AB (theo mẫu).
b) Vẽ đường thẳng CD đi qua điểm H và vuông góc với đường thẳng AB.
c) Vẽ đường thẳng EG đi qua điểm H và song song với đường thẳng AB.