Giúp mk vs.Cảm ơn mn nhiều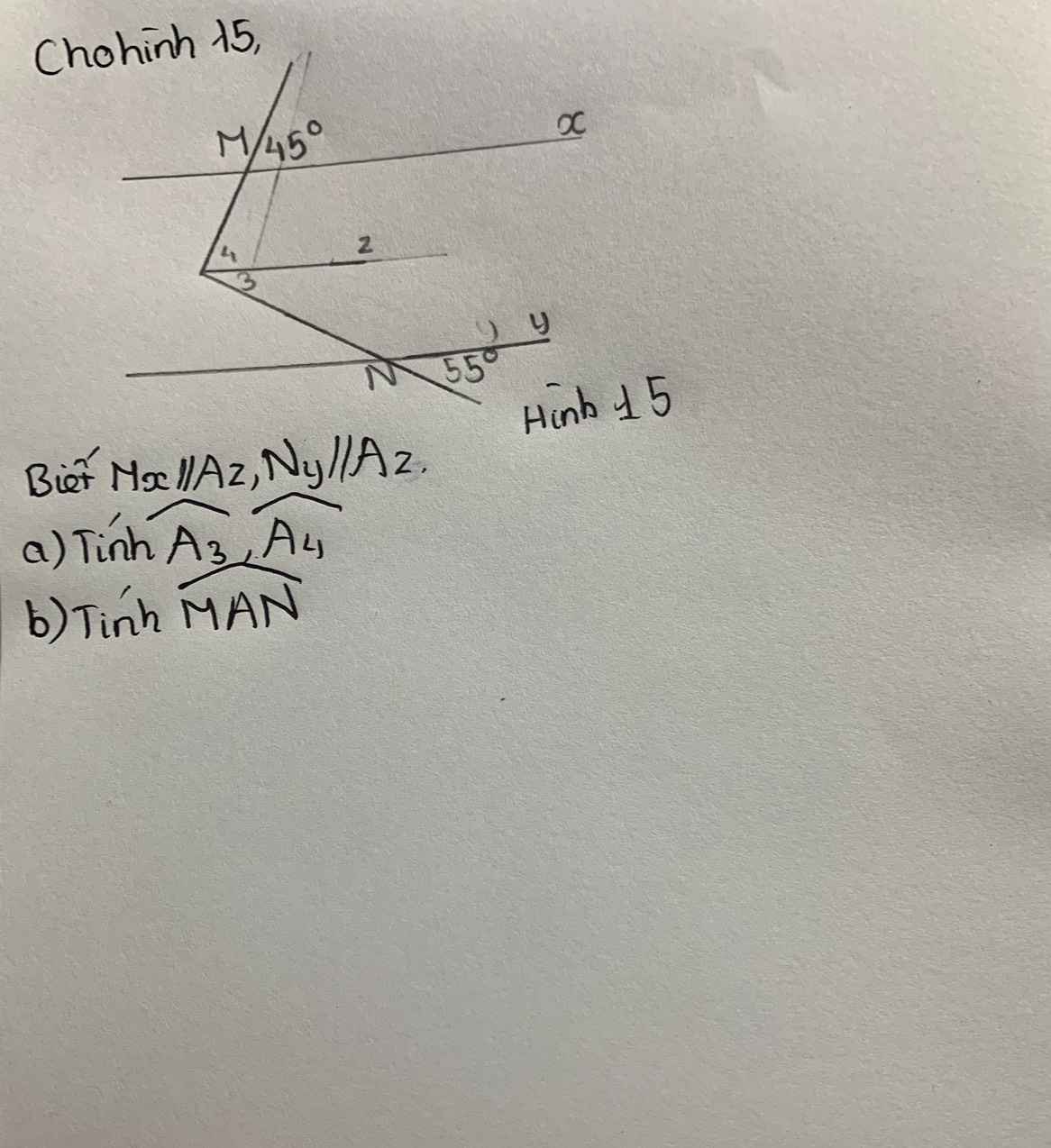

Những câu hỏi liên quan
Mn giúp mình giải bài 4 này vs.cảm ơn nhiều
Khái niệm phân loại câu theo cấu tạo
Giúp Mk vs.Cảm ơn mn
Khái niệm phân loại câu theo cấu tạo
Giúp Mk vs.Cảm ơn mn
Khái niệm phân loại câu theo cấu tạo
Giúp Mk vs.Cảm ơn mn
Câu bình thường : cấu tạo theo mô hình C- V
Câu đặc biệt : không cấu tạo theo mô hình C - V
Đúng 1
Bình luận (0)
Tìm một số tự nhiên có ba chữ số bt rằng nếu lấy số đó chia cho tổng các chữ số của nó thì được thương là 11.
Mn giải hộ mk vs.Cảm ơn mn nhìu ạ!!!
Giúp mình vs.Cảm ơn!
Đọc tiếp
Giúp mình vs.Cảm ơn!
Lời giải:
Gọi phân số cần tìm ban đầu là $\frac{a+14}{a}$
Theo bài ra ta có: $\frac{a+14+8}{a+8}=\frac{4}{3}$
$\frac{a+22}{a+8}=\frac{4}{3}$
$3(a+22)=4(a+8)$
$3a+66=4a+32$
$a=34$
Phân số cần tìm $\frac{34+14}{34}=\frac{48}{34}$
Đúng 1
Bình luận (1)
Giúp mình vs.Cảm ơn!!
Đọc tiếp
Giúp mình vs.Cảm ơn!!
Tìm phân số a/b,biết rằng nếu thêm 6 vào tử và thêm 21 vào mẫu của nó thì giá trị của phân số a/b ko đổi.Có bao nhiêu phân số như vậy?
Mn giải hộ mk vs.Cảm ơn mn nhìu lắm ạ.Ai làm nhanh mk sẽ tick cho.
Theo đề , ta có :
\(\frac{a}{b}\) = \(\frac{a+6}{b+21}\) => a.(b + 21) = (a + 6).b
=> ab + 21a = ab + 6b
=> 21a = 6b => a = \(\frac{6}{21}\)b
Vậy \(\frac{a}{b}\) = \(\frac{6}{21}\)
Đúng 1
Bình luận (0)
Ta có: \(\frac{a}{b}=\frac{a+6}{b+21}\Rightarrow a\left(b+21\right)=b\left(a+6\right)\)
\(ab+21a=ab+6b\)
\(21a=6b\)
\(\frac{a}{b}=\frac{6}{21}=\frac{3}{7}=\frac{3n}{7n}\)
Vậy có vô số phân số thỏa mãn với \(\frac{a}{b}=\frac{3n}{7n}\forall n\in Z\)
Đúng 1
Bình luận (0)
Các bạn ơi cho mk hỏi vòng 11 ioe lớp 7.Bài nghe có câu này:
We have four classes on * * * * * * * *
Mk nghe như từ SATURDAY nhưng mak người ta lại bảo sai.Vậy bn nào nghe đc chỉ mk vs.Cảm ơn nhiều!
Saturday đó em!(nhớ viết hoa chữ cái đâu thui!!)
Đúng 0
Bình luận (2)
Saturday ak.
Mk trả lời người ta bảo đúng mà.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mk với ạ, mk cảm ơn Mn nhiều 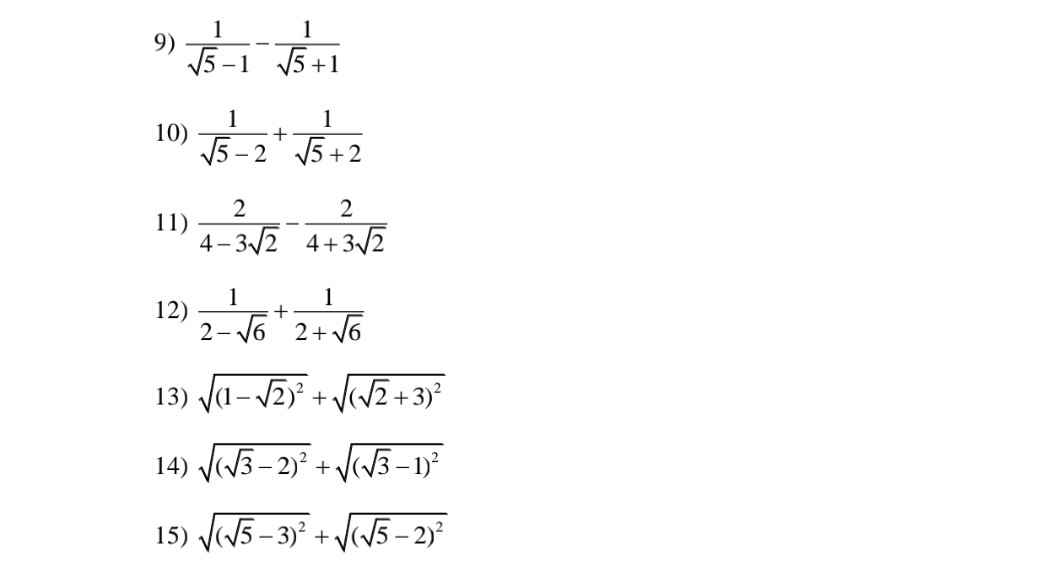
\(9,=\dfrac{\sqrt{5}+1-\sqrt{5}+1}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}=\dfrac{2}{4}=\dfrac{1}{2}\\ 10,=\dfrac{\sqrt{5}+2+\sqrt{5}-2}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}=2\sqrt{5}\\ 11,=\dfrac{8+6\sqrt{2}-8+6\sqrt{2}}{\left(4-3\sqrt{2}\right)\left(4+3\sqrt{2}\right)}=\dfrac{12\sqrt{2}}{-2}=-6\sqrt{2}\\ 12,=\dfrac{2+\sqrt{6}+2-\sqrt{6}}{\left(2-\sqrt{6}\right)\left(2+\sqrt{6}\right)}=\dfrac{4}{-2}=-2\\ 13,=\sqrt{2}-1+\sqrt{2}+3=2\sqrt{2}+2\\ 14,=2-\sqrt{3}+\sqrt{3}-1=1\\ 15,=3-\sqrt{5}+\sqrt{5}-2=1\)
Đúng 0
Bình luận (0)


















