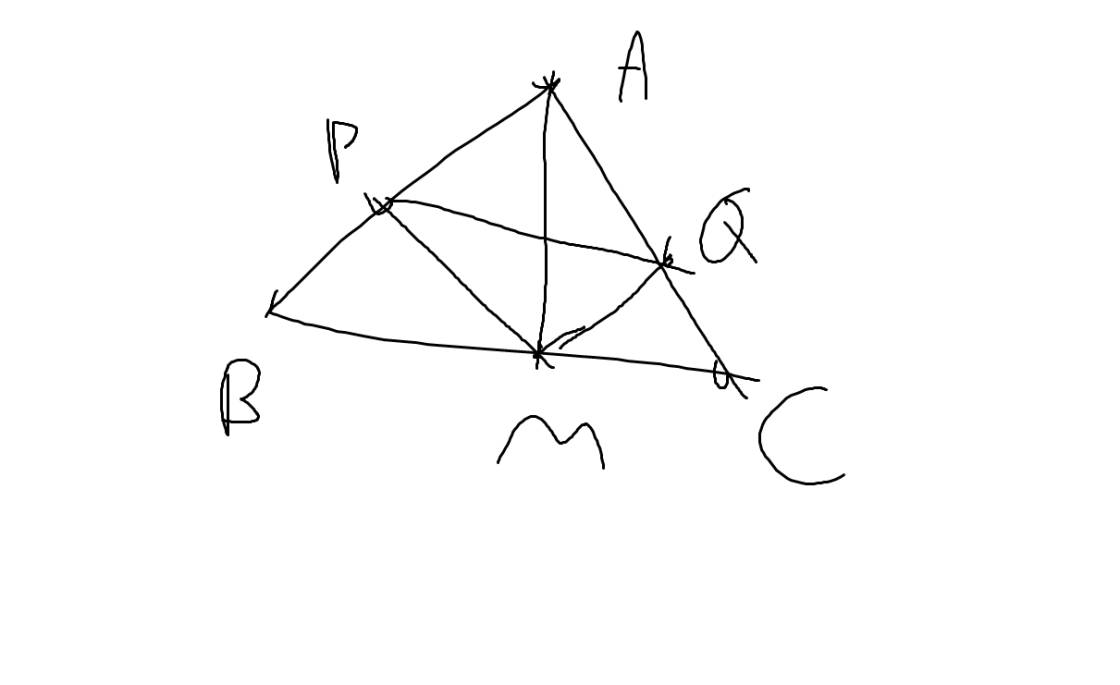
Tam giác ABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P,Q sao cho AP=CQ. Từ P vẽ PM song song với BC. (M thuộc AB).
a) Chứng minh PCMQ là hình chữ nhật
b) Gọi I là trung điểm MQ. CHứng minh rằng khi P di chuyển trên cạnh AC; Q di chuyển trên cạnh BC thì I di chuyển trên một đoạn thẳng cố định.

Những câu hỏi liên quan
#Toán_8 CÁC anh chị (các bạn ) giải giúp em mấy bài này với!Bài 1: Tam giác ABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P,Q sao cho APCQ. Từ P vẽ PM song song với BC. (M thuộc AB).a) Chứng minh PCMQ là hình chữ nhật b) Gọi I là trung điểm MQ. CHứng minh rằng khi P di chuyển trên cạnh AC; Q di chuyển trên cạnh BC thì I di chuyển trên một đoạn thẳng cố định.Bài 2: CHo tam giác ABC. Gọi O là một điểm thuộc miền trong tam giác. M ,N,P,Q lần lượt là trung điểm các đoạn OB , OC, AC và...
Đọc tiếp
#Toán_8 CÁC anh chị (các bạn ) giải giúp em mấy bài này với!
Bài 1: Tam giác ABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P,Q sao cho AP=CQ. Từ P vẽ PM song song với BC. (M thuộc AB).
a) Chứng minh PCMQ là hình chữ nhật
b) Gọi I là trung điểm MQ. CHứng minh rằng khi P di chuyển trên cạnh AC; Q di chuyển trên cạnh BC thì I di chuyển trên một đoạn thẳng cố định.
Bài 2: CHo tam giác ABC. Gọi O là một điểm thuộc miền trong tam giác. M ,N,P,Q lần lượt là trung điểm các đoạn OB , OC, AC và AB.
a) CM MNPQ là hình bình hành
b) Xác định vị trí của O để MNPQ là hình chữ nhật.
Bài 3: Cho tam giác ABC (AB<AC) . Trên AB lấy điểm D. Trên AC lấy điểm E sao cho BD=CE. Gọi I ; K lần lượt là trung điểm của BC và DE. Kéo dài IK cắt AB; AC lần lượt tại M và N. CMR: tam giác AMN cân.
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M Î AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Chứng minh: PM = CQ
Mà PM//CQ
Þ PCQM là hình bình hành
Lại có: C ^ = 90 0
Þ PCQM là hình chữ nhật

Đúng 0
Bình luận (0)
Send help!!!
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP bằng CQ. Từ điểm P vẽ PM song song BC ( M thuộc AB ). Cm tứ giác PCMQ là hình chữ nhật.
Cảm ơn nhiều nha
Bài 5. Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các
điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M ∈ AB).
Chứng minh tứ giác PCQM là hình chữ nhật.
a) có PM// CB (gt) => Góc APM = Góc C = 90 độ
=> tam giác APM vuông
Tam giác ABC vuông cân tại C => góc A = Góc B = 45 độ
Mà tam giác APM vuông có Góc A + góc AMP = 90 độ
=> Góc AMP= 45 độ = Góc A
=> Tam giác APM vuông cân tại P
=> AP = AM mà AP = CQ ( gt)
=> PM= CQ
b) Có PM // CB ( gt) hay PM // CQ
TG PMQC có PM= QC
PM // QC
=> TG PMQC là Hình bình hành mà góc C= 90 độ
=> TG PMQC là hình chữ nhật
Cho tam giác ABC vuông cân tại C. Trên AC, BC lần lượt lấy các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM // BC (M thuộc AB). a) Chứng minh PM = CQ b) Chứng minh tứ giác PCQM là hình chữ nhật
Bài 1: Tam giác ABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P,Q sao cho AP=CQ. Từ P vẽ PM song song với BC. (M thuộc AB).
a) Chứng minh PCMQ là hình chữ nhật
b) Gọi I là trung điểm MQ. CHứng minh rằng khi P di chuyển trên cạnh AC; Q di chuyển trên cạnh BC thì I di chuyển trên một đoạn thẳng cố định.
Cho tam giác ABC vuông cân tại C trên cạnh AC BC lấy lần lượt lấy các điểm P Q sao cho Ac = CD từ điểm B vẽ BM song song với BC M thuộc AB Chứng minh pcqm là hình chữ nhật(vẽ luôn hình aa)
Để chứng minh PCQM là hình chữ nhật, ta cần chứng minh 4 đỉnh P,, Q, M đều thuộc một đường thẳng và đường thẳng đó vuông góc với cả hai đường PQ và CM.Ta sẽ chứng minh từng bước như sau:Bước 1: Chứng minh P, C, Q thẳng hàngVì tam giác ABC vuông cân tại C và BM song song với BC, nên theo thuộc tính tam giác vuông cân và tam giác đồng dạng:- Ta có AC = BC (tam giác vuông cân)- Ta có BM || BC (theo giả thiết)- Ta có ∠ABC = ∠BAC (tam giác vuông cân)Do đó, tam giác ABC đồng dạng với tam giác BPC (theo góc). Từ đó, ta có:∠BPC = ∠ACB = 90° - ∠ABC = 90° - ∠BAC = ∠BCA (do tam giác vuông cân)Vậy ta có P, C,
Đúng 0
Bình luận (0)
1, Cho hình thang cân ABCD (AB //, AB CD). Gọi M, N, P, Q lần lượt là trung điểm các đoạn thẳng AD, BD, AC, BC .a, Chứng minh 4 điểm M, N, P, Q thẳng hàng .b, Chứng minh tứ giác ABPN là hình thang cân.c, Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật2, Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB .a, Chứng minh tứ giác MNPQ là hình bình hành.b, Xác định vị trí của điểm O Để tứ giác MNPQ là h...
Đọc tiếp
1, Cho hình thang cân ABCD (AB //, AB < CD). Gọi M, N, P, Q lần lượt là trung điểm các đoạn thẳng AD, BD, AC, BC .
a, Chứng minh 4 điểm M, N, P, Q thẳng hàng .
b, Chứng minh tứ giác ABPN là hình thang cân.
c, Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật
2, Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB .
a, Chứng minh tứ giác MNPQ là hình bình hành.
b, Xác định vị trí của điểm O Để tứ giác MNPQ là hình chữ nhật
3, Cho tam giác ABC Vuông cân tại C. Trên các cạnh AC , BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm B vẽ PM // BC ( M thuộc AB) Chứng minh tứ giác PCQM là hình chữ nhật
M.N VẼ HÌNH GIÚP LUÔN NHÉ. THANKS NHIỀU Ạ
Bài khá dài đó.
Sorry nhé mik mới lớp 6 ak nên ko bít, tha lỗi nha!
ý kiến gì thì nhắn tin cho mik mai 7g
pp, ngủ ngon!
Đúng 0
Bình luận (0)
Bạn Nữ hoàng Elsa lửa bn k biết thì đừng trả lời nhé
Đúng 0
Bình luận (0)
làm j phải căng bn với nhau mà chơi cho hòa đồng và đừng có chảnh nhé
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC.
Xem chi tiết
a, Chứng minh rằng MP = MQ và AP = AQ.
b, Đường thẳng PQ có vuông góc với AM không? Vì sao?
VẼ HÌNH GIÚP MÌNH NHA. CẢM ƠN Ạ
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ
Đúng 2
Bình luận (0)


















