Cho tam giác ABC, đường cao BM và CN cắt nhau tại H. CMR : \(MN=BC.cos\widehat{A}\)

Những câu hỏi liên quan
Cho tam giác \(ABC\) nhọn có hai đường cao \(BM,CN\) cắt nhau tại \(H\).
a) Chứng minh rằng \(\Delta AMN\backsim\Delta ABC\).
b) Phân giác của \(\widehat {BAC}\) cắt \(MN\) và \(BC\) lần lượt tại \(I\) và \(K\). Chứng minh rằng \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\).
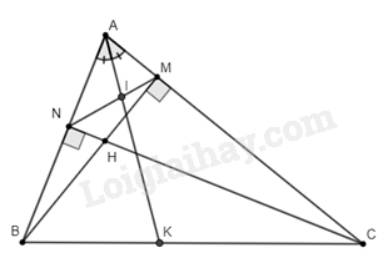
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, có hai đường cao BM và CN cắt nhau tại H.
a) CMR: AM. AC = AN. AB
b) Chứng minh hai tam giác AMN và ABC đồng dạng
c) Gọi P là giao điểm của AH với BC. CMR: PH là phân giác của góc MPN
d) Đường thẳng MN cắt BC tại D. CMR: DN. PM = DM. PN
a: Xet ΔAMB vuông tại M và ΔANC vuông tại N có
góc MAB chung
=>ΔAMB đồng dạng với ΔANC
=>AM/AN=AB/AC
=>AM*AC=AN*AB; AM/AB=AN/AC
b: Xet ΔAMN và ΔABC co
AM/AB=AN/AC
góc A chung
=>ΔAMN đồng dạng với ΔABC
c: góc MPH=góc ACN
góc NPH=góc ABM
góc ACN=góc ABM
=>góc MPH=góc NPH
=>PH là phân giác củagóc MPN
Đúng 2
Bình luận (0)
cho tam giác abc cân tại A, Các đường trung tuyến BM và CN
a)CMR: tam giác BMC=CNB
b)CMR: MN//BC
c)BM cắt CN tại G. CMR: AG vuông góc MN
vì tgiac ABC cân tại A
có BM và CN là trung tuyến=> AM=MC=AN=NB
a, xét tgiac BMC và tgiac CNB có:
BC là cạnh chung
góc B= góc C(gt)
BM=CN(cmt)
vậy tgiac BMC=Tgiac CNB(c.g.c)
b. xét tgiac AMN có AM=AN(cmt)
=> tgiac AMN cân tại đỉnh A
ta lại có tgiac ABC cân tại A
Vậy góc ANM= góc ABC= (180-góc A):2
mà góc ANM và góc ABC ở vị trí đồng vị => MN//BC
Đúng 0
Bình luận (0)
c.ta có BM cắt CN tại G=> G là trọng tâm tgiac ABC=> AG là đường trung tuyến ứng vơi cạnh BC
mà tamgiac ABC cân tại A nên đường trung tuyến AG cũng là đường cao vậy AG vuông góc với BC
mà BC//MN nên AG vuông góc với MN(từ vuông góc đến //)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC có các đường cao BM và CN cắt nhau tại H. Cho AH cắt BC tại K. Gọi I và O là tđ của AH và BC
Chứng minh \(\widehat{NIM}+\widehat{NOM=}180\)
Cho tam giác nhọn ABC .Hai đường cao BM cà CN của tam giác ABC cắt nhau tại H,biết BM=CN
a, Chứng minh tam giác ABC cân tại A
b,Chứng minh MN vuông góc với AH
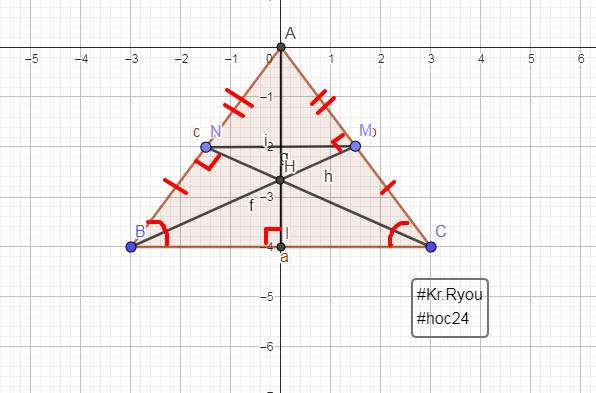
Cho tam giác ABC cân tại A,kẻ hai đường cao BM và CN cắt nhau tại H.Chứng minh rằng:
1)Tam giác ABM=tam giác ACN
2)Tam giác BMC=Tam giác CNB
3)AMN là tam giác gì
4) MN song song với BC
`@` `\text {Ans}`
`\downarrow`
`1)`
Vì `\Delta ABC` cân tại A.
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABM` và `\Delta ACN`:
`\text {AB = AC}`
$\widehat {A} \text { chung}$
$\widehat {ANC} = \widehat {AMB} (=90^0)$
`=> \Delta ABM = \Delta ACN (ch-gn)`
`2)`
Xét `2 \Delta` vuông `BMC` và `CNB`:
$\widehat {B} = \widehat {C}$
`\text {BC chung}`
`=> \Delta BMC = \Delta CNB (ch-gn)`
`3)`
Vì `\Delta BMC = \Delta CNB (b)`
`-> \text {BN = CM (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{AB = AN + NB}\\\text{AC = AM + MC}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BN = CM}\end{matrix}\right.\)
`-> \text {AM = AN}`
Xét `\Delta AMN`:
`\text {AM = AN}`
`-> \Delta AMN` cân tại A.
`4)`
Kẻ đường cao AI
Vì AI đi qua MN
`-> \text {AI} \bot \text {MN}`
Ta có: \(\left\{{}\begin{matrix}\text{AI }\bot\text{ MN}\\\text{AI }\bot\text{ BC}\end{matrix}\right.\)
`@` Theo tiên đề euclid
`-> \text {MN // BC}`
Hoặc bạn có thể giải cách này
Vì `\Delta AMN` cân tại A
\(\rightarrow\widehat{\text{AMN}}=\widehat{\text{ANM}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(1)`
Vì `\Delta ABC` cân tại A
\(\rightarrow\widehat{\text{ABC}}=\widehat{\text{ACB}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(2)`
Từ `(1)` và `(2)`
`->` \(\widehat{\text{ABC}}=\widehat{\text{ANM}}\)
Mà `2` góc này ở vị trí sole trong
`-> \text {MN // BC (t/c 2 đt' //).}`
Đúng 4
Bình luận (2)
1: Xét ΔABM vuông tại M và ΔACN vuông tại N có
AB=AC
góc BAM chung
=>ΔABM=ΔACN
2: Xét ΔNBC vuông tại N và ΔMCB vuông tại M có
BC chung
góc NBC=góc MCB
=>ΔNBC=ΔMCB
3: Xét ΔAMN có AM=AN
nên ΔAMN cân tại A
4: AM/AC=AN/AB
=>MN//BC
Đúng 1
Bình luận (0)
cho tam giác ABC có 3 góc nhọn, đường cao BM và CN cắt nhau tại H
a) cmr: tam giác HMB đồng dạng với tam giác HMC
b) cmr: AB.AN=AC.AM và góc AMN= góc ABC
c) gọi E là trung điểm của MN, K là trung điểm của BC
CMR EK ⊥ MN
d) chứng minh BN.BA+CM.CA=\(BC^2\)
Cho tam giác ABC có các đường cao AD,BE,CF cắt nhau tại H,kẻ BM,CN vuông góc với EF.Chứng minh DF+DE=MN
cho tam giác ABC nhọn đường cao BM,CN cắt nhau tại H.AH cắt BC tại I. CMR: IA là tia phân giác của góc MIN
B1:Cho tam giác ABC vuông tại A (AB<AC), đường phân giác BM. Trên tia đối của MB lấy D sao cho MB=MD. Qua D kể đường thẳng vuông góc với AC tại N và cắt BC tại E. Cmr: MN<MC
B2:Cho tam giác ABC cân tại A, AB=5cm, BC=6cm. Trung tuyến BM và CN cắt nhau tại G. E là điểm nằm giữa A và G. Cmr: AB-AM>EB-EM

















