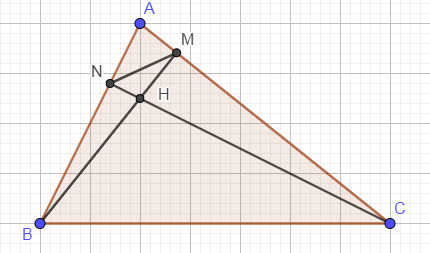
Ta có:
`hat(BNC) = hat(BMC)=90^o`
`=> BNMC` là tứ giác nội tiếp
`=>hat(ANM)=hat(ACB)` (cùng bù `hat(BNM)`)
`hat(AMB)=hat(ABC)`
Xét `ΔAMN` và `ΔABC` ta có:
`hat(ANM)=hat(ACB)(cmt)`
`hat(AMB)=hat(ABC)(cmt)`
`=>` `ΔAMN` `∼` `ΔABC` `(g.g)`
`=>(AM)/(AB) = (MN)/(BC)`
`=>MN= (AM)/(AB) . BC = MN.cos hat(A)`
cho tam giác ABC nhọn đường cao BM,CN cắt nhau tại H.AH cắt BC tại I. CMR: IA là tia phân giác của góc MIN
Cho tam giác ABC nhọn nội tiếp đường tròn tâm Ở, 2 đường cao BM,CN của tam giác ABC cắt nhau tại H. CM:
a) Tứ giác BCMN nội tiếp.
b) ∆AMN~∆ABC
c) Tia AO cắt đường tròn tâm Ở tại K cắt MN tại I
d,CM Tứ giác BHCK là hình bình hành
Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiêp
cho tam giác ABC nhọn nội tiếp đường tròn (O), hai đường cao BM,CN của tam giác ABC cắt nhau tại H . chứng minh:
a. tứ giác BCMN nội tiếp. xác định tâm E của đường tròn ngoại tiếp tứ giác BCMN
b. tam giác AMN đồng dạng tam giác ABC
c. tia AO cắt đường tròn (O) tại K, cắt MN tại I . chứng minh: tứ giác BHCK là hình bình hành
d. chứng minh: AK vuông góc MN
Cho tam giác ABC nhọn (AC > AB), đường cao BE, CF cắt nhau tại H. Lấy M thuộc BC (BM = CM). Đường tròn (BFM) cắt đường tròn (CEM) tại N. CMR: MN, AB, AC đồng qui
cho tam giác ABC vuông tại A ( AB<AC) đường cao AH . gọi D,E lần lượt là hình chiếu vuông góc của H lên AB và AC. hai đường thẳng BC vad DE cắt nhau tại I.
a) cm: AH=DE
b)cmr" ID.IE=IB.TC
c) các đường thẳng HD, HE lân lượt cắt đường thẳng BA tại M và cmr BM//CN
cho tam giác ABC vuông tại A ( AB<AC) đường cao AH . gọi D,E lần lượt là hình chiếu vuông góc của H lên AB và AC. hai đường thẳng BC vad DE cắt nhau tại I.
a) cm: AH=DE
b)cmr" ID.IE=IB.TC
c) các đường thẳng HD, HE lân lượt cắt đường thẳng BA tại M và cmr BM//CN
cho tam giác ABC nhọn đường cao BM,CN cắt nhau tại H. CMR:
a, tứ giác AMHN nội tiếp
b, BCMN nội tiếp
c, AH cắt BC tại I. CMR: IA là tia phân giác của góc MIN.
mình cần giải gấp câu (c) còn câu a và b mình giải được rồi. Giúp mình với
Cho tam giác ABC có BM và CN là các đường cao, gọi BM và CN cắt nhau tại H.
a/ Chứng minh AH ⊥ BC tại K.
b/ Chứng minh bốn điểm A, N, H M cùng thuộc đường tròn, xác định tâm I của đường tròn.
c/ Chứng minh bốn điểm B, N, M, C cùng thuộc đường tròn, xác định tâm O của đường tròn.
d/ Chứng minh MI ⊥ MO.
giúp em bài này vời ạ
Vẽ hộ tớ cãi chỗ : " Đường thẳng BC cắt đường thẳng MN tại D."
Cho tam giác ABC nhọn nội tiếp đường tròn (O) (AB < AC). Gọi H là giao điểm của các đường cao AI, BM, CN của tam giác ABC. Đường thẳng BC cắt đường thẳng MN tại D.
