cho 2 góc xAy,x'By' cùng nhọn có cạnh Ã// Bx', Ay//By'. chứng minh xAy=x'By'

Những câu hỏi liên quan
Bài 8: Cho \(\widehat{xAy}\) và \(\widehat{x'By'}\) có cạnh tương ứng song song. Tính số đo mỗi góc, biết \(4.\widehat{xAy}=5.\widehat{x'By'}\)
Chứng minh rằng: Nếu hai góc nhọn xAy và zBt có Ax//Bz, Ay// Bt thì góc zBt=góc xAy
Bài 8: Cho widehat{xAy} và widehat{xBy}có cạnh tương ứng song song. Tính số đo mỗi góc, biết 4.widehat{xAy}5.widehat{xBy}
Hình tự vẽ nhé
Ai nhanh mk sẽ tick
Đọc tiếp
Bài 8: Cho \(\widehat{xAy}\) và \(\widehat{x'By'}\)có cạnh tương ứng song song. Tính số đo mỗi góc, biết \(4.\widehat{xAy}=5.\widehat{x'By'}\)
Hình tự vẽ nhé![]()
Ai nhanh mk sẽ tick![]()
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN MN.Đặt AB 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MNa) Chứng minh rằng OH a, HM AN, HN BN.b) Gọi Bx là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx; By). Chứng minh BK là phân giác của góc ∠xBy.C. Chứng minh điểm H nằm trên một đường tròn cố định.
Đọc tiếp
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN = MN.
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AN, HN = BN.
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx'; By). Chứng minh BK là phân giác của góc ∠x'By.
C. Chứng minh điểm H nằm trên một đường tròn cố định.
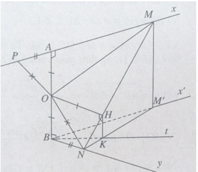
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
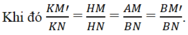
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)
Đúng 0
Bình luận (0)
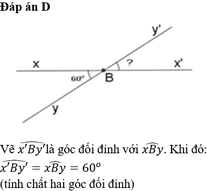
Cho góc xBy đối đỉnh với góc x'By' và góc xBy = 60°. Tính số đo góc x'By'
A. 30°
B. 120°
C. 90°
D. 60°
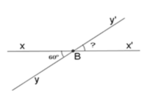
Vì ∠xBy là góc đối đỉnh với ∠x'By'. Khi đó: ∠xBy = ∠x'By' = 60° (tính chất hai góc đối đỉnh)
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho góc xBy đối đỉnh với góc x'By' và x B y ^ = 60 o . Tính số đo góc x'By'
A. 30 °
B. 120 °
C. 90 °
D. 60 °
vẽ góc nhọn xay . trên tia ã lấy hai điểm b và c ( b nằm giữa a và c ) trên tia ay lấy hai điểm d và e sao cho ad = ab , ae= ac
a, chứng minh be = dc
b, gọi o là giao điểm của be và dc . chứng minh tam giác obc bằng tam giác ode
c, vẽ trung điểm m của ce . chứng minh am là đg trung ttruwcj của ce
a) Xét ΔABE và ΔADC có
AB=AD(gt)
\(\widehat{DAC}\) chung
AE=AC(gt)
Do đó: ΔABE=ΔADC(c-g-c)
Suy ra: BE=DC(hai cạnh tương ứng)
b) Ta có: ΔABE=ΔADC(cmt)
nên \(\widehat{ABE}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ABE}+\widehat{DBC}=180^0\)(hai góc kề bù)
và \(\widehat{ADC}+\widehat{ODE}=180^0\)(hai góc kề bù)
nên \(\widehat{OBC}=\widehat{ODE}\)
Xét ΔOBC và ΔODE có
\(\widehat{OBC}=\widehat{ODE}\)(cmt)
BC=DE
\(\widehat{OCB}=\widehat{OED}\)(ΔACD=ΔAEB)
Do đó: ΔOBC=ΔODE(g-c-g)
c) Ta có: AC=AE(gt)
nên A nằm trên đường trung trực của CE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MC=ME(M là trung điểm của CE)
nên M nằm trên đường trung trực của CE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của CE(đpcm)
Đúng 3
Bình luận (2)
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN MN
Đặt AB 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc của điểm O trên đường thẳng MN
a) Chứng minh rằng OH a, HM AM, HN BN
b) Gọi Bx là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx,By). Chứng minh BK là phân giác của góc xBy ?
c) Chứng minh điểm H nằm trên một đường tròn cố định ?
Đọc tiếp
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN = MN
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc của điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AM, HN = BN
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx',By). Chứng minh BK là phân giác của góc x'By ?
c) Chứng minh điểm H nằm trên một đường tròn cố định ?
Bài 2. Cho góc xAy. Lấy điểm B trên Ax, điểm D trên Ay sao cho AB AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE DC. Chứng minh AABC AADEBài 3. Cho góc nhọn xOy và tia Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Lấy điểm I thuộc tia Oz Chứng minh rằng a) AAOI ABOI b) AB 1 OIBài 4. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD AC a) Chứng minh ABAC ABAD b) Trên tia đối của tia AB lấy điểm M. Chứ...
Đọc tiếp
Bài 2. Cho góc xAy. Lấy điểm B trên Ax, điểm D trên Ay sao cho AB = AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh AABC = AADE
Bài 3. Cho góc nhọn xOy và tia Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Lấy điểm I thuộc tia Oz Chứng minh rằng a) AAOI = ABOI b) AB 1 OI
Bài 4. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC a) Chứng minh ABAC = ABAD b) Trên tia đối của tia AB lấy điểm M. Chứng minh AMBD = AMBC
Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC
Đúng 1
Bình luận (0)