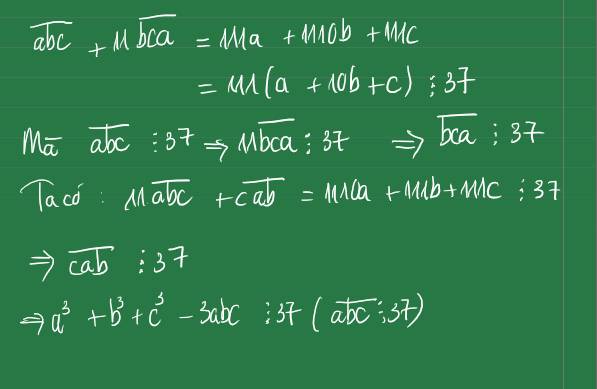Chứng minh rằng: nếu \(\overline{abc}\)\(⋮\)37 thì \(\overline{cab}\)\(⋮\)37

Những câu hỏi liên quan
Chứng minh rằng nếu \(\overline{abc⋮}37\) thì \(\overline{cab}⋮37\) và \(\overline{bca}⋮37\)
Cho \(\overline{abc}\) ⋮ 37 . Chứng minh rằng \(\overline{cab}\) ⋮ 37
(abc) chia hết cho 37
->100.a + 10.b + c chia hết cho 37
-> 1000.a + 100.b + 10.c chia hết cho 37
-> 1000.a - 999.a + 100.b + 10.c chia hết cho 37 (vì 999.a chia hết cho 37)
-> 100.b + 10.c + a = (bca) chia hết cho 37 (bca) chia hết cho 37
-> 100.b+10.c+a chia hết cho 37
-> 1000.b + 100.c + 10.a chia hết cho 37
-> 1000.b - 999.b + 100.c + 10.a chia hết cho 37 (vì 999.b chia hết cho 37)
-> 100.c + 10.a + b = (cab) chia hết cho 37
Đúng 3
Bình luận (0)
Chứng minh rằng số tự nhiên có 3 chữ số là \(\overline{abc}\) và \(\overline{cab}\)chia hết cho 37 thì số \(\overline{bca}\) cũng chia hết cho 37
Giả sử 3 số tự nhiên \(\overline{abc}\), \(\overline{bca}\), \(\overline{cab}\) đều chia hết cho 37. Chứng minh rằng:
a3+b3+c3-3abc cũng chia hết cho 37.
chứng minh rằng : Nếu abc chia hết cho 37 thì bca chia hết cho 37
(abc) chia hết cho 37=> 100.a + 10.b + c chia hết cho 37
=> 1000.a + 100.b + 10.c chia hết cho 37
=> 1000.a - 999.a + 100.b + 10.c chia hết cho 37 (vì 999.a chia hết cho 37)
=> 100.b + 10.c + a = (bca) chia hết cho 37
Đúng 0
Bình luận (0)
Chứng minh rằng nếu abc \(⋮\) 37 thì cab \(⋮\)37 và bca\(⋮\)37
Làm hộ mình với ạ. Mình cảm ơn=))
Chứng minh rằng ( đưa các lũy thừa về cùng cơ số rồi đặt thừa số chung)
7) \(\overline{abc}\) + \(\overline{bca}\) + \(\overline{cab}\) \(⋮\) 37
\(\overline{abc}+\overline{bca}+\overline{cab}=\left(100a+10b+c\right)+\left(100b+10c+a\right)+\left(100c+10a+b\right)\)
\(=111\left(a+b+c\right)=37\times3\times\left(a+b+c\right)⋮37\)
Đúng 0
Bình luận (0)
a, Cho \(\overline{abc}\)\(⋮\)37 . Chứng mình rằng : \(\overline{cab}\)\(⋮\)37
b, Tìm số x,y nguyên biết x.y + 12 = x+y
a) Do : \(\overline{abc}⋮37\)
\(\Leftrightarrow100a+10b+c⋮37\)
\(\Rightarrow1000a+100b+10c⋮37\)
Lại có : \(999a⋮37\)
\(\Rightarrow1000a-999a+100b+10c⋮37\)
\(\Leftrightarrow100b+10c+a⋮37\)
\(\Leftrightarrow1000b+100c+10a⋮37\)
\(\Leftrightarrow1000b-999b+100c+10a⋮37\)
\(\Leftrightarrow100c+10a+b⋮37\)
hay : \(\overline{cab}⋮37\) (ddpcm)
b) Ta có : \(xy+12=x+y\)
\(\Leftrightarrow x+y-xy=12\)
\(\Leftrightarrow x\left(1-y\right)-\left(1-y\right)=11\)
\(\Leftrightarrow\left(x-1\right)\left(1-y\right)=11\)
Do đó : x-1 và y-1 là các cặp ước của 11
Rồi bạn lập bảng xét các ước của 11.
a.Xét tổng\(11.\overline{abc}+\overline{cab}\)ta có:
\(11.\overline{abc}+\overline{cab}=1110a+111b+111c=111\left(10a+b+c\right)=37.3\left(10a+b+c\right)⋮37\)
Mà \(11.\overline{abc}⋮37\Rightarrow\overline{cab}⋮37\)
xy+12=x+y
\(\Rightarrow xy-x-y=12\)
\(\Rightarrow x\left(y-1\right)-\left(y-1\right)=12+1\)
\(\Rightarrow\left(x-1\right)\left(y-1\right)=13\)
Mà x,y nguyên nên ta có bảng sau:
| x-1 | 1 | -1 | 13 | -13 |
| y-1 | 13 | -13 | 1 | -1 |
| x | 2 | 0 | 14 | -12 |
| y | 14 | -12 | 2 | 0 |
Vây...........
Xem thêm câu trả lời
Chứng minh rằng:
a) Nếu \(\overline{abc}\)+ \(\overline{deg}\)\(⋮\)37 thì \(\overline{abcdeg}\)\(⋮\)37
b) Nếu 2a + 3b + c \(⋮̸\)7 thì \(\overline{abc}\)\(⋮̸\)7
a) Giả sử abcdeg chia hết cho 37 —> 999abc+(abc+deg) chia hết cho 37
—> 999abc chia hết cho 37 vì 999 :37 ko dư —>abc + deg chia hết cho 37
Đúng 0
Bình luận (0)