vẽ (P) : y= \(2x^2\) và đường thẳng (d) : y= x + 1 trên cùng một hệ trục toạ độ
Những câu hỏi liên quan
câu 1: a) vẽ parabol (p): y 1/2x^2 và đường thẳng (d): y3/2x-1 trên cùng 1 mặt phẳng toạ độb) xác định toạ độ giao điểm của (p) và (d) bằng phép toáncâu 2: a) vẽ đồ thị hàm số (p): yx^2 và (d): Y-x+2 trên cùng 1 hệ trục toạ độb) xác định toạ độ giao điểm của (p) và (d)câu 3: cho hai hàm số yx^2 và y-2x+3a) vẽ các đồ thị của hai hàm số này trên cùng một hệ trục toạ độb) tìm toạ độ giao điểm của hai đồ thị đó
Đọc tiếp
câu 1: a) vẽ parabol (p): y= 1/2x^2 và đường thẳng (d): y=3/2x-1 trên cùng 1 mặt phẳng toạ độ
b) xác định toạ độ giao điểm của (p) và (d) bằng phép toán
câu 2: a) vẽ đồ thị hàm số (p): y=x^2 và (d): Y=-x+2 trên cùng 1 hệ trục toạ độ
b) xác định toạ độ giao điểm của (p) và (d)
câu 3: cho hai hàm số y=x^2 và y=-2x+3
a) vẽ các đồ thị của hai hàm số này trên cùng một hệ trục toạ độ
b) tìm toạ độ giao điểm của hai đồ thị đó
a, vẽ đồ thị hàm số y = \(\dfrac{x^2}{2}\) và đường thẳng (d) : y = x + 4 trên cùng một hệ trục toạ độ
b, tìm toạ độ giao diểm P và d bằng phép tính
trên cùng một hệ trục toạ độ , cho 3 đường thẳng (d1) (d2) (d3) lần lượt là đồ thị hàm số y=-2x+2,6=1/2x-3 và y=mx+n a)vẽ đồ thị (d1) (d2) trên cùng một hệ trục toạ độ b)tìm m,n để đường thẳng (d3) song song với (₫1) cắt (d2j tại điểm có tung ddoj bằng -1
Cho hai đường thẳng: (d1):y=1/2x+2 và (d2):y=-x+2
a) vẽ (d1) và (d2) trên cùng một hệ trục toạ độ Oxy
b) gọi A là giao điểm của (d1) với trục hoành. Tìm toạ độ điểm A
c) gọi B là giao điểm của (d2) với trục tung. Tìm toạ đồ điểm B
d)gọi C là giao điểm của (d1) và (d2). Tìm toạ độ điểm C
Mông các bạn giải giúp mình gấp với ạ :3
a/ bạn tự làm
b/ \(\Rightarrow y=0\Rightarrow\dfrac{1}{2}x+2=0\) giải PT tìm hoành độ x
c/ \(\Rightarrow x=0\Rightarrow y=0+2=2\)
d/ \(\Rightarrow\dfrac{1}{2}x+2=-x+2\) Giải PT tìm hoành độ x của C rồi thay vào d1 hoặc d2 để tìm tung độ y của C
Đúng 0
Bình luận (0)
Cho hai hàm số : y = x^2 (p) ; y = x + 2 (d) a) vẽ đồ thị hai hàm số trên tron cùng một hệ trục toạ độ b) tìm toạ độ giao điểm của (p) và (d) c) tìm m để đường thẳng : y=2x-m cắt (p) tại hai điểm phân biệt nằm về hai phía đối với trục tung
a: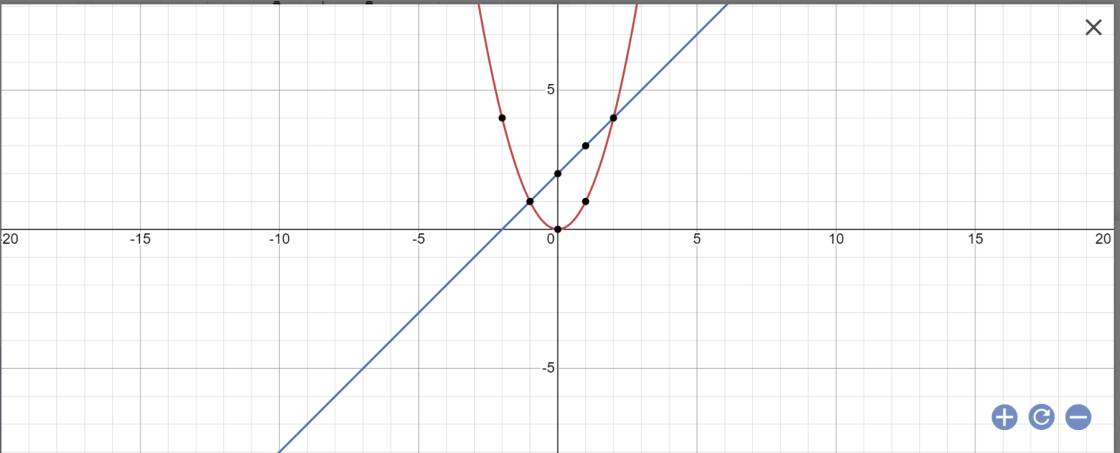 
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
c: PTHĐGĐ là:
x^2-2x+m=0
Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0
Đúng 1
Bình luận (1)
Bài 1 cho parabol (P): y x2 và đường thẳng d: y 1/2xa) vẽ đồ thị của (P) và d trên cùng hệ trục toạ độb) xác đingj toạ độ giao điểm của (P) và dc) Dựa vào đồ thị, hãy giải bất phương trình x2 lớn hơn hoặc bằng 1/2xBài 2 Cho parabol (P): y 2x2 và đường thẳng d: y x + 1a) vẽ (P) và d trên cùng hệ trục toạ độb) Tìm toạ độ giao điểm của (P) và dc) Dựa vào đồ thị, hãy giải bất phương trình 2x2 - x - 1 0
Đọc tiếp
Bài 1 cho parabol (P): y= x2 và đường thẳng d: y= 1/2x
a) vẽ đồ thị của (P) và d trên cùng hệ trục toạ độ
b) xác đingj toạ độ giao điểm của (P) và d
c) Dựa vào đồ thị, hãy giải bất phương trình x2 lớn hơn hoặc bằng 1/2x
Bài 2 Cho parabol (P): y= 2x2 và đường thẳng d: y= x + 1
a) vẽ (P) và d trên cùng hệ trục toạ độ
b) Tìm toạ độ giao điểm của (P) và d
c) Dựa vào đồ thị, hãy giải bất phương trình 2x2 - x - 1 < 0
Vẽ trên cùng một hệ trục toạ độ đồ thị của hai hàm số: y = 2x (d1) và y = - x + 3(d2) b/ Đường thẳng (d2) cắt (d1) tại A và cắt trục Ox tại B. Tìm toạ độ các điểm A, B và tính diện tích tam giác AOB ( đơn vị trên các trục toạ độ là xentimét ).
\(b,\text{PT giao Ox của }\left(d_2\right):y=0\Leftrightarrow-x+3=0\Leftrightarrow x=3\Leftrightarrow B\left(3;0\right)\Leftrightarrow OB=3\\ \text{PTHĐGĐ }\left(d_1\right)\text{ và }\left(d_2\right):2x=-x+3\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\\ \text{Gọi }H\text{ là đường cao từ }A\text{ của }\Delta OAB\\ \Rightarrow AH=\left|y_A\right|=2\\ \Rightarrow S_{OAB}=\dfrac{1}{2}AH\cdot OB=\dfrac{1}{2}\cdot2\cdot3=3\left(đvdt\right)\)
Đúng 0
Bình luận (0)
Cho hàm số y = 2x và y = - 3x + 5
a. vẽ trên cùng một hệ trục toạ độ
b. tìm toạ độ giao điểm M của hai đường thẳng y = 2x và y = -3x + 5
c. đường thẳng kẻ qua điểm (0;4), // Ox cắt đường thẳng : y = 2x và y = -3x + 5 ở P và Q. Xác định toạ độ P và Q
a) Vẽ trên cùng hệ trục toạ độ Oxy đồ thị các hàm số sau:
y = x (d)
y = 2x (d2)
y = -x + 3 (d3)
b) Đường thẳng (d3) cắt các đường thẳng (d1), (d2) theo thứ tự tại A, B. Tìm toạ độ của các điểm A, B và tính diện tích tam giác OAB.
Trong mặt phẳng toạ độ Oxy cho đường thẳng (d1): y=-x+2 và (d2): y=1/4x
1. Vẽ (d1) và (d2) trên cùng hệ trục toạ độ Oxy
2. Lấy điểm B trên (d2) có hoành độ bằng -4. Viết phương trình đường thẳng (d3) song song với (d1) và qua điểm B
3. Tìm toạ độ giao điểm của (d1) và (d2) bằng phép tính
Xem chi tiết