cho a b c là độ dài 3 cạnh tam giác p là nửa chu vi ab/(p-c) + bc/(p-a) + ca/(p-b)>=4p

Những câu hỏi liên quan
cho a b c là độ dài 3 cạnh tam giác p là nửa chu vi chứng minh ab/(p-c) + bc/(p-a) + ca/(p-b)>=4p
Cho tam giác ABC ngoại tiếp đường tròn (I). Các cạnh AB, BC, CA tiếp xúc đường tròn (I) lần lượt tại D, E, F. Đặt BC a, CA b, AB ca, Chứng minh AD
b
+
c
-
a
2
b, Gọi r là bán kính của (I). Chứng minh
S
A
B
C
p.r, trong...
Đọc tiếp
Cho tam giác ABC ngoại tiếp đường tròn (I). Các cạnh AB, BC, CA tiếp xúc đường tròn (I) lần lượt tại D, E, F. Đặt BC = a, CA = b, AB = c
a, Chứng minh AD =
b
+
c
-
a
2
b, Gọi r là bán kính của (I). Chứng minh S A B C = p.r, trong đó p là nửa chu vi tam giác ABC
c, Gọi M là giao điểm của đoạn thẳng AI với (I). Tính độ dài đoạn thẳng BM theo a, b, c
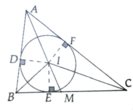
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b
Đúng 0
Bình luận (0)
Cho a,b,c là độ dài ba cạnh của một tam giác có chu vi là 3:
CMR: \(\sqrt{\frac{ab}{a+b-c}}+\sqrt{\frac{bc}{b+c-a}}+\sqrt{\frac{ca}{c+a-b}}\ge3\)
Do a,b,c là 3 cạnh tam giác nên \(a+b-c>0;b+c-a>0;c+a-b>0\)
Đặt \(x=b+c-a>0\)
\(y=a+c-b>0\)
\(z=a+b-c>0\)
\(\Rightarrow a=\frac{"y+z"}{2}\)
\(\Rightarrow b=\frac{"x+z"}{2}\)
\(\Rightarrow c=\frac{"x+y"}{2}\)
\(A=\frac{a}{"b+c-a"}+\frac{b}{"a+c-b"}+\frac{c}{"a+b-c"}\)
\(=\frac{"y+z"}{"2x"}+\frac{"x+z"}{"2y"}+\frac{"x+y"}{"2z"}\)
\(=\frac{1}{2}."\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}"\)
Áp dụng công thức bdt Cauchy cho 2 số :
\(\frac{x}{y}+\frac{y}{x}\ge2\)
\(\frac{x}{z}+\frac{z}{x}\ge2\)
\(\frac{y}{z}+\frac{z}{y}\ge2\)
Cộng 3 bdt trên, suy ra :
\("\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}"\ge6\)
\(\Rightarrow A\ge\frac{1}{2}.6=3\) "dpcm"
P/s: Nhớ thay thế dấu ngoặc kép thành dấu ngoặc đơn nhé
Đúng 0
Bình luận (0)
cho tam giác ABC có độ dài cạnh AB bằng 12cm. tổng độ dài 2 cạnh BC và CA hơn độ dài cạnh AB là 7cm
a/ tìm tổng độ dài hai cạnh BC và CA
b/tính chu vi hình tam giác ABC
a. Tổng BC và CA là:
12 + 7= 19(cm)
b. Chu vi tam giác ABC là:
12 + 19= 31(cm)
Đ/s: a: 19cm
b:31cm
Cho a, b, c là ba cạnh tam giác, gọi p là nửa chu vi. CMR:
\(2p\le\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\)
\(\hept{\begin{cases}\frac{ab}{c}+\frac{bc}{a}\ge2b\\\frac{bc}{a}+\frac{ca}{b}\ge2c\\\frac{ca}{b}+\frac{ab}{c}\ge2a\end{cases}}\) :)))
Cho tam giác ABC có đường tròn nội tiếp tiếp xúc với 3 cạnh AB, BC, CA theo thứ tự tại M, N, P. Biết AB=c, BC=a, AC=b và p là nửa chu vi tam giác ABC. Tỉ số AM/MB tính theo a,b,c,p bằng?
Cho a,b,c là độ dài 3 cạnh tam giác, p là nửa chu vi, cmr:
\(\dfrac{a}{p-a} + \dfrac{b}{p-b} + \dfrac{c}{p-c} >= 6\)
BĐT\(\Leftrightarrow\dfrac{a}{-a+b+c}+\dfrac{b}{a-b+c}+\dfrac{c}{a+b-c}\ge3\)
Áp dụng BĐT Svac-xơ, ta có:
\(\dfrac{a^2}{-a^2+ab+ac}+\dfrac{b^2}{ab-b^2+bc}+\dfrac{c^2}{ac+bc-c^2}\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)-\left(a^2+b^2+c^2\right)}\)
Ta có: \(a,b,c\) là 3 cạnh của 1 tam giác nên:
\(a\left(b+c\right)>a^2\). Tương tự và cộng theo vế, ta có:
\(2\left(ab+bc+ca\right)-\left(a^2+b^2+c^2\right)>0\)
Ta sẽ chứng minh \(\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)-\left(a^2+b^2+c^2\right)}\ge3\left(1\right)\)
Thật vậy, \(BĐT\left(1\right)\Leftrightarrow3\left(a^2+b^2+c^2\right)+\left(a+b+c\right)^2\ge6\left(ab+bc+ca\right)\), đúng
Đẳng thức xảy ra khi và chỉ khi \(a=b=c\)
Đúng 1
Bình luận (0)
Cách 2:
Đặt \(\left\{{}\begin{matrix}-a+b+c=x\\a-b+c=y\\a+b-c=z\end{matrix}\right.\) với \(x,y,z>0\)
Khi đó ta có \(a=\dfrac{y+z}{2};b=\dfrac{x+z}{2};c=\dfrac{x+y}{2}\)
BĐT cần chứng minh trở thành:
\(\dfrac{y+z}{x}+\dfrac{x+z}{y}+\dfrac{x+y}{z}\ge6\), đúng theo bđt Cauchy
Đẳng thức xảy ra khi và chỉ khi \(x=y=z\Leftrightarrow a=b=c\)
Đúng 1
Bình luận (2)
a,b,c là độ dài 3 cạnh của 1 tam giác chu vi bằng 1 cmr
\(\frac{b+c-a}{a^2+bc}+\frac{c+a-b}{b^2+ca}+\frac{a+b-c}{c^2+ab}>4\)
Cho a,b,c là độ dài 3 cạnh của 1 tam giác có chu vi bằng 1. C/m rằng: ab+ac+bc>a.b.c
Vì a, b, c là độ dài của 3 cạnh tam giác \(\Rightarrow a,b,c>0\)
Do chu vi của tam giác bằng 1 \(\Rightarrow a+b+c=1\Rightarrow b+c=1-a\)
Giả sử : \(ab+ac+bc>a\cdot b\cdot c\)
\(\Rightarrow ab+ac+bc-abc>0\)
\(\Rightarrow a\left(b+c\right)+bc\left(1-a\right)>0\Rightarrow a\left(b+c\right)+bc\left(b+c\right)>0\)
\(\Rightarrow\left(b+c\right)\left(a+bc\right)>0\)( thỏa mãn vì \(a,b,c>0\))
Vậy \(ab+bc+ac>a\cdot b\cdot c\)( ĐPCM )


















