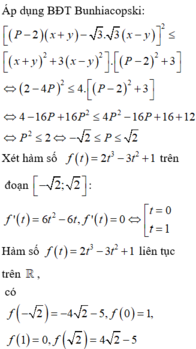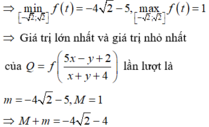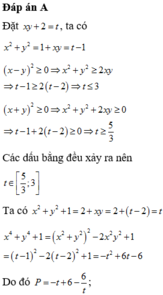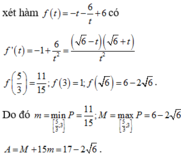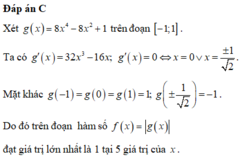Cho các số thực ko âm x,y thỏa mãn x+y+xy=8 , hãy tím giá trị nhỏ nhất của M=x2+y2

Những câu hỏi liên quan
Cho x , y là các số thực dương thỏa mãn x + y + xy = 8 . Tìm giá trị nhỏ nhất của biểu thức A = x2 + y2
Cho các số thực x, y thỏa mãn x2 + y2 = 8. Giá trị nhỏ nhất của S = x + y bằng:
\(\left(x+y\right)^2\le2\left(x^2+y^2\right)=16\)
\(\Rightarrow x+y\ge-4\)
\(S_{min}=-4\)
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
2
(
x
2
+
y
2
)
+
x
y
(
x
+
y
)
(
x
y
+
2
)
Giá trị nhỏ nhất của biểu thức
P
4
(
x
3
y
3...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( x y + 2 ) Giá trị nhỏ nhất của biểu thức P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 )
A. - 25 4
B. 5
C. -13
D. - 23 4
Đáp án D
Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0 (*)
Đặt x + y = u x y = v ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0 gải ra ta được u = v + 2 + v 2 + 28 v + 4 4
Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18 , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18 ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0 với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 ) trong đó t 0 = m i n t = m i n ( x y + y x ) với x,y thỏa mãn điều kiện (*).
Ta có :
t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2
Vậy m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4
Đúng 0
Bình luận (0)
Cho các số thực x, y thay đổi thỏa mãn
x
2
+
y
2
-
x
y
1
và hàm số
f
t
2
t
3
-
3
t
2
-
1
. Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của
Q
f...
Đọc tiếp
Cho các số thực x, y thay đổi thỏa mãn x 2 + y 2 - x y = 1 và hàm số f t = 2 t 3 - 3 t 2 - 1 . Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của Q = f 5 x - y + 2 x + y + 4 . Tổng M + m bằng
A. - 4 - 3 2
B. - 4 - 5 2
C. - 4 - 4 2
D. - 4 - 2 2
Cho x, y là những số thực thỏa mãn
x
2
–
x
y
+
y
2
1
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
4
+
y
4
+
1
x...
Đọc tiếp
Cho x, y là những số thực thỏa mãn x 2 – x y + y 2 = 1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 4 + y 4 + 1 x 2 + y 2 + 1 . Giá trị của A = M + 15 m là
A. A = 17 - 2 6
B. A = 17 - 6
C. A = 17 + 6
D. A = 17 + 2 6
Cho x,y là những số thực thỏa mãn
x
2
-
x
y
+
y
2
1
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
4
+
y
4
+
1
x
2
+
y...
Đọc tiếp
Cho x,y là những số thực thỏa mãn x 2 - x y + y 2 = 1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 4 + y 4 + 1 x 2 + y 2 + 1 . Giá trị của A = M + 15m là
A. A = 17 - 2 6
B. A = 17 + 6
C. A = 17 + 2 6
D. A = 17 - 6
Cho các số thực x, y, z thay đổi và thỏa mãn điều kiện
x
2
+
y
2
+
z
2
1
. Giá trị nhỏ nhất của biểu thức
P
x
y
+
y
z
+
2
x
z...
Đọc tiếp
Cho các số thực x, y, z thay đổi và thỏa mãn điều kiện x 2 + y 2 + z 2 = 1 . Giá trị nhỏ nhất của biểu thức P = x y + y z + 2 x z 2 − 8 x + y + z 2 − x y − y z + 2
A. min P = − 5
B. min P = 5
C. min P = 3
D. min P = − 3
Đáp án D
Ta có C 12 1 . C 10 1 = 120
Khi đó C 12 1 . C 10 1 = 120 . Đặt C 12 1 . C 10 1 = 120
Ta luôn có C 12 1 . C 10 1 = 120
C 12 1 . C 10 1 = 120 Suy ra C 12 1 . C 10 1 = 120
Xét hàm số f t = t 2 − 8 t + 3 trên khoảng − 1 ; + ∞ ,có f ' t = 2 t + 1 2 t + 4 t + 3 2 > 0 ; ∀ t > − 1
Hàm số f(t) liên tục trên − 1 ; + ∞ ⇒ f t đồng biến trên − 1 ; + ∞
Do đó, giá trị nhỏ nhất của f(t) là min − 1 ; + ∞ f t = f − 1 = − 3 . Vậy P min = − 3
Đúng 0
Bình luận (0)
Cho các số thực x,y không âm thỏa mãn điều kiện x2+y2≤2�2+�2≤2.Hãy tìm giá trị lớn nhất của biểu thức P√x×(29x+3y)+√y×(29y+3x).
Đọc tiếp
Cho các số thực x,y không âm thỏa mãn điều kiện .Hãy tìm giá trị lớn nhất của biểu thức .
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2\leq (x+y)[(29x+3y)+(29y+3x)]=32(x+y)^2\leq 32.(x^2+y^2)(1+1)=64(x^2+y^2)\leq 64.2=128$
$\Rightarrow P\leq 8\sqrt{2}$
Vậy $P_{\max}=8\sqrt{2}$
Đúng 0
Bình luận (0)
Cho các số thực x, y thỏa mãn x2 + y2 = 1. Giá trị nhỏ nhất của S = x + y bằng:
\(\left(x+y\right)^2\le2\left(x^2+y^2\right)=2\)
\(\Rightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)
\(S_{min}=-\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho x, y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
P
x
2
+
y
2
+
2
(
x
+
1
)
(
y
+
1
)
+
8
4
-
x
-...
Đọc tiếp
Cho x, y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y Tính giá trị M + m
A. 41
B. 44
C. 42
D. 43