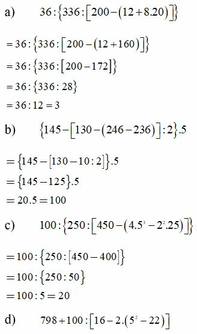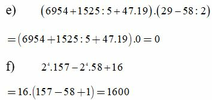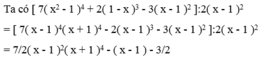Thực hiện phép chia 236 cho 12.
Những câu hỏi liên quan
Thực hiện các phép cộng sau:
(- 12) + (- 48); (-236) + (- 1025).
(-12) + (-48) = - (12 + 48) = -60
(-236) + (-1 025) = - (236 + 1 025) = -1 261
Đúng 0
Bình luận (0)
Thực hiện phép tính:
248+(-12)+2012+(-236)
= 248 + 2012 + ( -12 ) + ( -236 )
= 2260 + ( -12 ) + ( -236 )
= 2248 + ( -236 )
= 2012
Đúng 0
Bình luận (0)
SGK Toán 4 tập 1 - Bộ sách Chân trời sáng tạo - Trang 16
13 tháng 9 2023 lúc 11:05
a) Thực hiện các phép chia sau rồi xác định các phép chia hết, các phép chia có dư.10 : 211 : 2 22 : 213 : 214 : 225 : 236 : 217 : 258 : 229 : 2 b) Các số chia hết cho 2 có tận cùng là chữ số nào?Các số không chia hết cho 2 có tận cùng là chữ số nào?
Đọc tiếp
a) Thực hiện các phép chia sau rồi xác định các phép chia hết, các phép chia có dư.
10 : 2 11 : 2 | 22 : 2 13 : 2 | 14 : 2 25 : 2 | 36 : 2 17 : 2 | 58 : 2 29 : 2 |
b) Các số chia hết cho 2 có tận cùng là chữ số nào?
Các số không chia hết cho 2 có tận cùng là chữ số nào?
a, 10:2 = 5 (Phép chia hết)
22: 2= 11 (Phép chia hết)
14:2=7 (Phép chia hết)
36:2= 18 (Phép chia hết)
58:2= 29 (Phép chia hết)
11:2=5 (dư 1)
13:2=6 (dư 1)
25:2= 12 (dư 1)
17:2= 8 (dư 1)
29:2= 14 (dư 1)
b, Các số chia hết cho 2 có tận cùng là các chữ số 0;2;4;6;8
Các số không chia hết cho 2 có tận cùng là các chữ số 1;3;5;7;9
Đúng 2
Bình luận (0)
Thực hiện phép tính:a)
36
:
336
:
200
-
12
+
8
.
20
b)
145
-
130...
Đọc tiếp
Thực hiện phép tính:
a) 36 : 336 : 200 - 12 + 8 . 20
b) 145 - 130 - 246 - 236 : 2 . 5
c) 100 : 250 : 450 - 4 . 5 3 - 2 2 . 25
d) 798 + 100 : 16 - 2 . 5 2 - 22
e) 6954 + 1525 : 5 + 47 . 19 . 29 - 58 : 2
f) 2 4 . 157 - 2 4 . 58 + 16
Bạn Tân thực hiện phép chia một số cho 12 thì dư 1 và chia số đó cho 14 thì dư 2. Bạn hãy chứng tỏ Tân đã làm sai ít nhất một phép tính.
A = 12 x p + 1 = 14 x q + 2 (với p ; q là số tự nhiên)
Ta thấy : 12 x p là số chẵn nên A = 12 x p + 1 là số lẻ.
14 x q là số chẵn nên A = 14 x q + 2 là số chẵn.
A không thể vừa lẻ vừa chẵn nên chắc chắn có ít nhất một phép tính sai.
Đúng 0
Bình luận (0)
Thực hiện các phép chia sau
7
x
2
-
1
4
+
2
1
-
x
3
-
3
x
-...
Đọc tiếp
Thực hiện các phép chia sau 7 x 2 - 1 4 + 2 1 - x 3 - 3 x - 1 2 : 2 x - 1 2
Bạn Tân thực hiện phép chia 1 số cho 12 thì dư 1 và chia số đó cho 14 thì dư 2. Bạn hãy chứng tỏ Tân đã làm sai ít nhất một phép tính
Gọi số đó là A thì A = 12 x p + 1 = 14 x q + 2 ( với p, q là số tự nhiên )
Ta thấy:
* 12 x p là số chẵn nên
A = 12 x p + 1 là số lẻ
* 14 x q là số chẵn nên
A = 14 x q + 2 là số chẵn
* A không thể vừa là số lẻ vừa là số chẵn nên chắc chắn có ít nhất một phép tính sai
Đúng 0
Bình luận (0)
Bạn Tân thực hiện phép chia một số cho 12 thì dư 1 và chia số đó cho 14 thì dư 2. Bạn hãy chứng tỏ Tân đã làm sai ít nhất một phép tính
gọi số đó là A thì A=12*p+1=14*q+2
ta thấy
12*p là số chẵn nên (1)A=12*p+1 là số lẻ
14*q là số chẵn nênA=14*q+2 là số chẵn (2)
Từ (1) và (2)=>đpcm
Đúng 0
Bình luận (0)
Gọi số đó là A thì A = 12x p + 1 = 14 x q + 2 ( p và q là số tự nhiên )
Ta thấy
- 12 x p là số chẵn nên
= >12 x p + 1 là số lẻ
- 14 x q là số chẵn nên
=> 14 x
Đúng 0
Bình luận (0)
nữa nha mk thiếu :
=> 14 x q + 2 là số chẵn
=> đpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bạn Tân thực hiện phép chia một số hco 12 thì dư 1 và chia số đó cho 14 thì dư 2. Hãy chứng tỏ Tân đã làm sai một phép tính.
Gọi số đó là A thì A = 12 x p + 1 = 14 x q + 2 ( với p, q là số tự nhiên )
Ta thấy:
* 12 x p là số chẵn nên
A = 12 x p + 1 là số lẻ
* 14 x q là số chẵn nên
A = 14 x q + 2 là số chẵn
* A không thể vừa là số lẻ vừa là số chẵn nên chắc chắn có ít nhất một phép tính sai
Đúng 0
Bình luận (0)
Gọi số đó là A thì A = 12 x p + 1 = 14 x q + 2 ( với p, q là số tự nhiên )
Ta thấy:
* 12 x p là số chẵn nên
A = 12 x p + 1 là số lẻ
* 14 x q là số chẵn nên
A = 14 x q + 2 là số chẵn
* A không thể vừa là số lẻ vừa là số chẵn nên chắc chắn có ít nhất một phép tính sai
Trong câu hỏi tương tự
Đúng 0
Bình luận (0)
Bạn Tân thực hiện phép chia một số cho 12 thì dư 1 và chia số đó cho 14 thì dư 2. Bạn hãy chứng tỏ Tân đã làm sai ít nhất một phép tính.
chia 12 dư 1 nghĩa rằng ssoo đó là số lẻ
chia 14 dư 2 nghĩa là số đó là số chắn=> mâu thuẫn có ít nhất 1 phép tính sai
Đúng 0
Bình luận (0)
Gọi số đó là A thì A = 12 x p + 1 = 14 x q + 2 ( với p, q là số tự nhiên )
Ta thấy:
* 12 x p là số chẵn nên
A = 12 x p + 1 là số lẻ
* 14 x q là số chẵn nên
A = 14 x q + 2 là số chẵn
* A không thể vừa là số lẻ vừa là số chẵn nên chắc chắn có ít nhất một phép tính sai
Đúng 0
Bình luận (0)