Trong bài toán ở phần mở đầu, ta gọi \(x,y\) lần lượt là số lạng thịt bò và số lạng thịt cá mà bác An ăn trong một ngày. Viết hệ thức liên hệ giữa \(x\) và \(y\) để đáp ứng nhu cầu bổ sung protein của bác An.

Những câu hỏi liên quan
Trong 1 lạng (100 g thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu 46 g protein. (Nguồn: https://vinmec.com và https://thanhnien.vn) Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.
Đọc tiếp
Trong 1 lạng (100 g thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu 46 g protein. (Nguồn: https://vinmec.com và https://thanhnien.vn) Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.
- Bước 1: Biểu diễn lượng protein có trong x lạng thịt bò và y lạng cá rô phi.
Lượng protein trong x lạng thịt bò là 26x (g)
Lượng protein trong y lạng cá rô phi là 20y (g)
Lượng protein trong x lạng thịt bò và y lạng cá rô phi là 26x+20y (g).
- Bước 2: Biểu diễn bất phương trình.
Vì lượng protein tối thiểu là 46g nên ta có bất phương trình:
\(26x + 20y \ge 46\)
- Bước 3: Tìm nghiệm của bất phương trình
Thay x=1, y=1 vào bất phương trình ta được
Thay x=2, y=1 vào bất phương trình ta được
Thay x=1, y=2 vào bất phương trình ta được
Vậy (1;1), (2;1), (1;2) là các nghiệm cần tìm.
Chú ý
Có thể chọn các nghiệm khác, miền là nghiệm nguyên.
Đúng 0
Bình luận (0)
Nhu cầu canxi tối thiểu cho một người đang độ tuổi trưởng thành trong một ngày là 1300 mg. trong 1 lạng đậu nành có 165 mg canxi, 1 lạng thịt có 15 mg canxi.(Nguồn: https://hongngochospital.vn)Gọi x,y lần lượt là số lạng đậu nành và số lạng thịt mà một người đang độ tuổi trưởng thành ăn trong một ngàya) Viết bất phương trình bậc nhất hai ẩn x,y để biểu diễn lượng canxi cần thiết trong một ngày của một người trong độ tuổi trưởng thành.b) Chỉ ra một nghiệm left( {{x_0};{y_0}} right) với {x_0},{y_0...
Đọc tiếp
Nhu cầu canxi tối thiểu cho một người đang độ tuổi trưởng thành trong một ngày là \(1300\) mg. trong 1 lạng đậu nành có 165 mg canxi, 1 lạng thịt có 15 mg canxi.
(Nguồn: https://hongngochospital.vn)
Gọi \(x,y\) lần lượt là số lạng đậu nành và số lạng thịt mà một người đang độ tuổi trưởng thành ăn trong một ngày
a) Viết bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng canxi cần thiết trong một ngày của một người trong độ tuổi trưởng thành.
b) Chỉ ra một nghiệm \(\left( {{x_0};{y_0}} \right)\) với \({x_0},{y_0} \in \mathbb{Z}\) của bất phương trình đó.
a)
Lượng canxi có trong x lạng đậu nành là 165x (mg)
Lượng canxi có trong y lạng thịt là 15y (mg)
Bất phương trình là \(165x + 15y \ge 1300\)
b) Thay cặp số (10;10) vào bất phương trình ta được:
\(165.10 + 15.10 = 1650 + 150\)\( = 1800 > 1300\)
Vậy (10;10) là một nghiệm của bất phương trình.
Đúng 0
Bình luận (0)
Một gia đình cần ít nhất 900 đoen vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogram thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogram thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền của một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x, y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm...
Đọc tiếp
Một gia đình cần ít nhất 900 đoen vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogram thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogram thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền của một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x, y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính x 2 + y 2
A. x 2 + y 2 = 1 , 3
B. x 2 + y 2 = 2 , 6
C. x 2 + y 2 = 1 , 09
D. x 2 + y 2 = 0 , 58
Chọn đáp án A
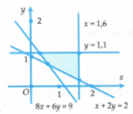
Gọi a, b lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua đảm bảo lượng protein và lipit trong thức ăn. Theo bài ra ta có số tiền gia đình cần trả là 160a + 110b với a, b thỏa mãn



Do đó, tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì x = a = 0,3; y = b = 1,1
![]()
Đúng 0
Bình luận (0)
Cho biết mỗi 100 g thịt bò chứa khoảng 26,1 g protein, một quả trứng nặng 44 g chứa khoảng 5,7 g protein (nguồn: https://www.vinmec.com). Giả sử có một người mỗi ngày cần không quá 60 g protein. Gọi số gam thịt bò và số quả trứng mà người đó ăn trong một ngày lần lượt là x và y.a) Lập bất phương trình theo x, y diễn tả giới hạn về lượng protein trong khẩu phần ăn hằng ngày của người đó.b) Dùng bất phương trình ở câu a) để trả lời hai câu hỏi sau:- Nếu người đó ăn 150 g thịt bò và 2 quả trứng (mỗ...
Đọc tiếp
Cho biết mỗi 100 g thịt bò chứa khoảng 26,1 g protein, một quả trứng nặng 44 g chứa khoảng 5,7 g protein (nguồn: https://www.vinmec.com). Giả sử có một người mỗi ngày cần không quá 60 g protein. Gọi số gam thịt bò và số quả trứng mà người đó ăn trong một ngày lần lượt là x và y.
a) Lập bất phương trình theo x, y diễn tả giới hạn về lượng protein trong khẩu phần ăn hằng ngày của người đó.
b) Dùng bất phương trình ở câu a) để trả lời hai câu hỏi sau:
- Nếu người đó ăn 150 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày thì có phù hợp không?
- Nếu người đó ăn 200 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày thì có phù hợp không?
a) Mỗi gam thịt bò chứa 0,261 g protein.
Người đó ăn x gam thịt bò, tương ứng 0,261.x g protein
Mỗi quả trứng nặng 44 g chứa 5,7 g protein.
Người đó ăn y quả trứng, tương ứng 5,7.x g protein
Như vậy lượng protein trong khẩu phần ăn hằng ngày của người đó là: \(0,261x + 5,7y\)
Mỗi ngày, người đó cần không quá 60 g protein nên ta có bất phương trình: \(0,261x + 5,7y \le 60\)
b)
- Nếu người đó ăn 150 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày thì lượng protein tương ứng: \(150.0,261 + 2.5,7 = 50,55 \le 60\) \( \Rightarrow \)Kết luận: phù hợp.
- Nếu người đó ăn 200 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày thì lượng protein tương ứng: \(200.0,261 + 2.5,7 = 63,6 > 60\) \( \Rightarrow \)Kết luận: Không phù hợp.
Đúng 0
Bình luận (0)
Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hoà loại hai chiều và một chiều mà cửa hàng cần nhập. Từ HĐ1, viết hệ bất phương trình hai ẩn x, y và chỉ ra một nghiệm của hệ này.
- Lập hệ:
Do số lượng máy nhập vào phải là số tự nhiên nên ta có \(x \ge 0,y \ge 0\).
Từ HĐ 1 ta có hai bất phương trình là \(x + y \le 100\) và \(2x + y \le 120\)
Vậy hệ bất phương trình từ HĐ 1 là
\(\left\{ \begin{array}{l}x + y \le 100\\2x + y \le 120\\x \ge 0\\y \ge 0\end{array} \right.\).
Cặp số (x;y)=(50;10) là một nghiệm của hệ BPT vì thay x= 50, y= 10 ta được:
\(\left\{ {\begin{array}{*{20}{l}}
{50 + 10 \le 100}\, \text {(Đúng)}\\
{2.50 + 10 \le 120}\, \text {(Đúng)}\\
{50 \ge 0}\, \text {(Đúng)}\\
{10 \ge 0}\, \text {(Đúng)}
\end{array}} \right.\)
Đúng 0
Bình luận (0)
Trong một cuộc thi về bữa ăn dinh dưỡng ban tổ chức yêu cầu để đàm bảo lượng dinh dưỡng hằng ngày thì mỗi gđ có 4 thành viên cần ít nhất 900 đvi protein và 400 đvi lipit, 1kg heo chứa 600 đvi protein và 400 đvi lipit, 1kg thịt bò chứa 800 đvi protein và 200 đvi lipit. Biết rằng giá 1kg thịt bò là 100000đ, 1kg thịt heo là 70000đ. Tìm chi phí thấp nhất cho khẩu phần thức ăn đảm bảo chất dinh dưỡng?
Đọc tiếp
Trong một cuộc thi về bữa ăn dinh dưỡng ban tổ chức yêu cầu để đàm bảo lượng dinh dưỡng hằng ngày thì mỗi gđ có 4 thành viên cần ít nhất 900 đvi protein và 400 đvi lipit, 1kg heo chứa 600 đvi protein và 400 đvi lipit, 1kg thịt bò chứa 800 đvi protein và 200 đvi lipit. Biết rằng giá 1kg thịt bò là 100000đ, 1kg thịt heo là 70000đ. Tìm chi phí thấp nhất cho khẩu phần thức ăn đảm bảo chất dinh dưỡng?
Hải mua 3 lạng thịt và 6 lạng cá hết 45 000 đồng.Dương mua 6 lạng thịt và 2 lạng cá cùng loại hết 55 000 đồng.Em hãy cho biết tổng số tiền để mua được 1 cân thịt và 1 cân cá cùng loại (theo giá 2 bạn mua)là bao nhiêu?
thịt là 10 000 đồng
cá là 5 000 đòng
mk ko chắc đâu
Đúng 0
Bình luận (0)
Mua 6 lạng thịt và 12 lạng cá hết số tiền là:45 000x2=90 000(đ)
Mua 1 cân cá hết số tiền là:90 000-55 000=35 000(đ)
Mua 6 lạng cá hết số tiền là:35 000:10x6=21 000(đ)
Mua 3 lạng thịt hết số tiền là:45 000-21000=24000(đ)
Mua 1 cân thịt hết số tiền là:24 000:3x10=80 000(đ)
Mua 1 cân thịt và 1 cân cá hết số tiền là:35 000+80 000=115 000(đ)
Đ/S:115 000 đ
Đúng 0
Bình luận (0)
Trong bài toán ở phần mở đầu, ta gọi x, y lần lượt là số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất (x, y là số tự nhiên). Nếu điều kiện ràng buộc đối với 1 và y để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về.
Đổi 60g=0,06kg, 50g=0,05kg
Lượng đường cần cho x chiếc bánh nướng là 0,06x kg
Lượng đường cần cho y chiếc bánh dẻo là 0,05y kg
Vì lượng đường đã nhập về là 500kg và lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về nên ta có:
\(0,06x + 0,05y \le 500\)
Đúng 0
Bình luận (0)
Một gia đình cần ít nhất 900g chất protein và 400g lipit trong thức ăn mỗi ngày. Biết rằng thịt bò chứ 80% protein và 20% lipit. Thịt lợn chứa 60% protein và 40% lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1600g thịt bò và 1100g thịt lợn, giá tiền 1kg thịt bò là 45000 đồng, 1kg thịt lợn là 35 nghìn đồng. Gia đình đó phải mua bao nhiêu kg thịt mỗi loại để chi phí là ít nhất
Đọc tiếp
Một gia đình cần ít nhất 900g chất protein và 400g lipit trong thức ăn mỗi ngày. Biết rằng thịt bò chứ 80% protein và 20% lipit. Thịt lợn chứa 60% protein và 40% lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1600g thịt bò và 1100g thịt lợn, giá tiền 1kg thịt bò là 45000 đồng, 1kg thịt lợn là 35 nghìn đồng. Gia đình đó phải mua bao nhiêu kg thịt mỗi loại để chi phí là ít nhất
Hải mua 3 lạng thịt lạc và 6 lạng cá hết 45000 đồng.Dương mua 6 lạng thịt và 2 lạng cá cùng loại hết 55000 đồng.Em hãy cho biết giá tiền 1 cân thịt và 1 cân cá (theo giá hai bạn mua) là ........ đồng
Giải tắt (ngắn gọn) 2 tick
Đáp số 1 tk
Giải đầy đủ,dễ hiểu 3 tk
Giúp mình nha mọi người
gọi số tiền 1 lạng thịt là x
gọi số tiền 1 lạng cá là y
theo bài ra ta có hpt:\(\hept{\begin{cases}3x+6y=45000\\6x+2y=55000\end{cases}}\)
=>\(\hept{\begin{cases}6x+12y=90000\\6x+2y=55000\end{cases}}\)=>\(\hept{\begin{cases}10y=35000\\3x+6y=45000\end{cases}}\)
=>\(\hept{\begin{cases}y=3500\\x=8000\end{cases}}\)
đúng 100%% giải theo cách lớp 9
Nhớ mk nha
Đúng 0
Bình luận (0)











