Hãy viết một phương trình bậc nhất hai ẩn và chỉ ra một nghiệm của nó.

Những câu hỏi liên quan
Tìm bất phương trình bậc nhất hai ẩn trong các bất phương trình sau và chỉ ra một nghiệm của bất phương trình bậc nhất hai ẩn đó:
a) \(5x + 3y < 20\)
b) \(3x - \frac{5}{y} > 2\)
a) \(5x + 3y < 20\)
Đây là bất phương trình bậc nhất hai ẩn.
Chọn \(x = 0;y = 0\)
Khi đó bất phương trình tương đương với 5.0+3.0
Vậy (0;0) là một nghiệm của bất phương trình trên.
b) \(3x - \frac{5}{y} > 2\)
Đây không là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.
Đúng 0
Bình luận (0)
Hãy chỉ ra phương trình bậc nhất một ẩn? Nếu là phương trình bậc nhất một ẩn thì nêu hệ số a và b?
a) x+2=0
b) x+x2=0
c) 1-2t=0
d) 3y=0
e) 0x-3=0
Các pt a,c,d và pt bậc nhất 1 ẩn
a: a=1; b=2
c: a=-2; b=1
d: a=3; b=0
Đúng 1
Bình luận (0)
pt bậc nhất : a ; c ; d ; d
a, x + 2 = 0 hệ số a = 1 ; b = 2
c, -2t + 1 = 0 hệ số a = -2 ; b = 1
d, 3y = 0 hệ số a = 3 ; b = 0
Đúng 1
Bình luận (0)
Cho bất phương trình bậc nhất hai ẩn \(x + 2y \ge 0\).
a) Hãy chỉ ra ít nhất hai nghiệm của bất phương trình trên.
b) Với y=0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?
a)
+) Thay x=0 và y=0 vào bất phương trình \(x + 2y \ge 0\), ta được:
\(0 + 2.0 \ge 0 \Leftrightarrow 0 \ge 0\)(Đúng)
=> (0;0) là một nghiệm của bất phương trình \(x + 2y \ge 0\)
+) Thay x=1, y=1 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(1 + 2.1 \ge 0 \Leftrightarrow 3 \ge 0\)(Đúng)
=> (1;1) là một nghiệm của bất phương trình \(x + 2y \ge 0\)
Ta tìm được 2 nghiệm của bất phương trình đã cho là (0;0) và (1;1).
b)
Thay y=0 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(x + 2.0 \ge 0 \Leftrightarrow x \ge 0\)
Ta thấy bất phương trình bài cho tương đương với bất phương trình nên số giá trị của x thỏa mãn bất phương trình đã cho là số x thỏa mãn điều kiện .
Mà ta có vô số giá trị của x thỏa mãn nên có vô số giá trị của x thỏa mãn bất phương trình đã cho.
Chú ý
Ta có thể thử các cặp số khác đối với câu a, miễn là cặp số đấy làm cho bất phương trình đúng.
Đúng 0
Bình luận (0)
Cho bất phương trình bậc nhất hai ẩn \(x - 2y + 6 > 0\)
a) (0;0) có phải là một nghiệm của bất phương trình đã cho không?
b) Chỉ ra ba cặp số (x;y) là nghiệm của bất phương trình đã cho.
c) Biểu diễn miền nghiệm của các bất phương trình đã cho trên mặt phẳng tọa độ Oxy
Tham khảo:
a) Vì \(0 - 2.0 + 6 = 6 > 0\) nên (0;0) là một nghiệm của bất phương trình đã cho.
b) Vì \(0 - 2.1 + 6 = 4 > 0\) nên (0;1) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.0 + 6 = 7 > 0\) nên (1;0) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.1 + 6 = 5 > 0\) nên (1;1) là một nghiệm của bất phương trình đã cho.
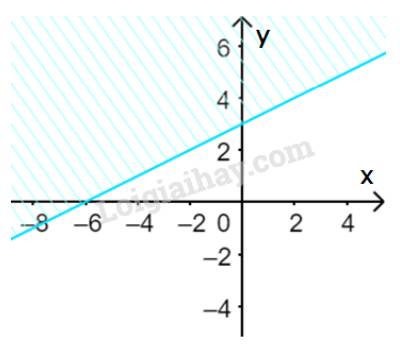
c) Vẽ đường thẳng \(\Delta :x - 2y + 6 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( { - 2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 2.0 + 6 = 6 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Đúng 0
Bình luận (0)
Cho phương trình 3x – 2y = 5
Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ có nghiệm duy nhất.
Ta có: 3x – 2y = 5 ⇔ 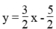
Để được một hệ có nghiệm duy nhất thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc khác 3/2 .
Chẳng hạn: 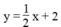 ⇔ -x + 2y = 4
⇔ -x + 2y = 4
Khi đó ta có hệ 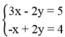 có một nghiệm duy nhất.
có một nghiệm duy nhất.
Đúng 0
Bình luận (0)
Cho hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x - y < 3\left( 1 \right)\\x + 2y > - 2\left( 2 \right)\end{array} \right.\)
a) Mỗi bát phương trình (1) và (2) có là bất phương trình bậc nhất hai ẩn không?
b) Chỉ ra một nghiệm chung của hai bất phương trình (1) và (2) trong hệ trên.
a) Hai bất phương trình bài cho là bất phương trình bậc nhất hai ẩn.
b) (1; 1) là một nghiệm chung của hai BPT (1) và (2) vì:
Thay x=1;y=1 vào (1) ta được: 1-1<3 (Luôn đúng)
Thay x=1; y=1 vào (2) ta được: 1+2.1>-2 (Luôn đúng)
Đúng 0
Bình luận (0)
Cho phương trình 3x – 2y = 5
Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ vô nghiệm.
Ta có: 3x – 2y = 5 ⇔ 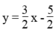
Để được một hệ vô nghiệm thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc bằng 3/2 và tung độ gốc khác - 5/2 .
Chẳng hạn: 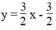 ⇔ 3x – 2y = 3
⇔ 3x – 2y = 3
Khi đó ta có hệ 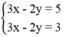 vô nghiệm.
vô nghiệm.
Đúng 0
Bình luận (0)
a)Hãy định nghĩa phương trình bậc nhất một ẩn?Phương trình : 2x – 5 = 3 + 2x có phải là phương trình bậc nhất một ẩn không ?
b)Tìm các giá trị của m sao cho phương trình :12 – 2(1- x)2 = 4(x – m) – (x – 3 )(2x +5) có nghiệm x = 3.
c)Định nghĩa hai phương trình tương đương ? Cho ví dụ. Giải thích.
a: Phương trình có dạng ax+b=0 khi a<>0 được gọi là phương trình bậc nhất một ẩn
Phương trình 2x-5=2x+3 là phương trình bậc nhất một ẩn
c: Hai phương trình tương đương là hai phương trình có cùng tập nghiệm
Đúng 3
Bình luận (0)
Cho phương trình 3x – 2y = 5
Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ có vô số nghiệm.
Ta có: 3x – 2y = 5 ⇔ 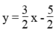
Để được một hệ có vô số nghiệm thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc bằng 3/2 và tung độ gốc bằng - 5/2 .
Chẳng hạn: 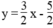 ⇔ 6x – 4y = 10
⇔ 6x – 4y = 10
Khi đó ta có hệ 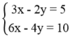 có vô số nghiệm.
có vô số nghiệm.
Đúng 0
Bình luận (0)
Cho x1, x2 là hai nghiệm của phương trình: x^2-2x-1=0.Hãy lập một phương trình bậc hai một ẩn có hại nghiệm là x1+(x2)^2 và x2+(x1)^2
\(x^2-2x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}u=x_1+\left(x_2\right)^2\\v=x_2+\left(x_1\right)^2\end{matrix}\right.\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}u+v=\left(x_1+x_2\right)+\left(x_2+x_1\right)^2-2x_1x_2\\uv=2x_1x_2+x_1^3+x_2^3=2x_1x_2+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=8\\uv=12\end{matrix}\right.\)
=>u và v là nghiệm của pt \(t^2-8t+12=0\)
Đúng 2
Bình luận (0)

















