Tìm 1 số có 4 chữ số ,biết nếu lấy số đó cộng với tổng các chữ số của nó thì được 2015.

Những câu hỏi liên quan
Số tự nhiên A được viết bởi 2015 chữ số 6. Hỏi nếu lấy A chia cho 15 thì số dư là bao nhiêu, nếu lấy thương là số tự nhiên ?Tìm một số tự nhiên có bốn chữ số. Biết rằng số đó cộng với tổng các chữ số của nó thì bằng 1993 .Trung bình cộng của hai số tự nhiên là 343. Tìm số lớn, biết rằng nếu thêm chữ số 4 vào bên phải số bé thì được số lớn ?
Xem chi tiết
Ta có : 6:15=0 dư 6
66:15=4 dư6
666:15=44 dư 6.....
vậy dư 6
Đúng 0
Bình luận (0)
1: tổng các chữ số là
2015 x 6 = 12090
tách 15=3 x 5 .mà 1209 chia hết cho3 và 5 vậy thì khi chia 15 ko dư
2 bạn đặt cột dọc chắc chắn phải là số 4 chữ số
ABCD+A+B+C+D=1993(ĐẶT NHƯ ĐẶT TÍNH RỒI TÍNH )
=> a =1 vì nếu = 2 sẽ >1993 và =0 thì ra số 3 chữ số
vậy BCD +B+C+D=1993-1000-1=992
b=8hay 9
b=8 thì cd+c+d =992-800-8=184
c=9
d+d =184-90-9=85c( ko chia hết cho 2 lần d nên sai)
b=9 cd+c+d=992-900-9=83
c=7 vì chỉ có 77 là nhỏ hơn 83 và để cho d là số 1 chữ số .d+d = 83-70-7=6
d =3 .SỐ ĐÓ LÀ 1973
3: TÔNG LÀ :343x2=686
SỐ LỚN LÀ :(686-4) /11=62
ĐÁP SỐ 624 ...... TẤT CẢ ĐÚNG ĐẤY
Đúng 0
Bình luận (0)
Tìm một số tự nhiên có 4 chữ số, biết rằng nếu lấy số đó cộng với tổng các chữ số
của nó thì được 2000.
Lời giải:
Gọi số cần tìm là $\overline{abcd}$ với $a,b,c,d\in\mathbb{N}; a,b,c,d\leq 9; a\neq 0$
Theo bài ra ta có:
$\overline{abcd}+a+b+c+d=2000(*)$
Suy ra $\overline{abcd}<2000$
Suy ra $a<2$. Do đó $a=1$
Thay vô $(*)$ ta có: $\overline{1bcd}+1+b+c+d=2000$
$1000+100\times b+10\times c+d+1+b+c+d=2000$
$101\times b+11\times c+2\times d=999$
Nếu $b=8$ thì $11\times c+2\times d=191$. Mà $11\times c+2\times d$ lớn nhất bằng $11\times 9+2\times 9=117$ nên vô lý.
Nếu $b<8$ thì $11\times c+2\times d$ càng lớn hơn $191$, càng vô lý.
Do đó $b=9$
Khi ấy: $11\times c+2\times d=90$
Nếu $c=6$ thì $2\times d=24$. Điều này vô lý do $2\times d$ lớn nhất bằng $18$
Nếu $c<6$ thì $2\times d$ càng lớn hơn $24$, càng vô lý.
Do đó $c=7,8,9$. Thay vào ta tìm được $d=1$ khi $c=8$.
Vậy số cần tìm là $1981$
Đúng 1
Bình luận (0)
Tìm 1 số có 4 chữ số biết rằng nếu lấy số đó cộng với tổng các chữ số của nó thì kết quả là 1993.
Gọi số cần tìm là abcd (a \(\ne\) 0 ;a,b,c,d là chữ số)
Ta có :
abcd + (a + b + c + d) = 1993
\(\Rightarrow\) 1000a + 100b + 10c + d + a + b + c + d = 1993
\(\Rightarrow\) 1001a + 101b + 11c + 2d = 1993
Vì 0 < a \(\le\) 9 nên a = 1 \(\Rightarrow\) 101b + 11c + 2d = 992
Vì b là chữ số :
- Nếu b \(\le\) 8 thì c,d sẽ không tồn tại do cùng là chữ số.
- Nếu b = 9 thì 11c + 2d = 83
Vì c là chữ số :
- Nếu c < 7 thì d không tồn tại do cùng là chữ số.
- Nếu c > 7 thì 11c > 83
- Nếu c = 7 thì 2d = 6 \(\Rightarrow\) d = 3.
Vậy số cần tìm là 1973
Đúng 0
Bình luận (0)
Gọi số cần tìm là abcd ( a khác 0 ; a,b,c,d là chữ số)
Ta có:
abcd + ( a + b + c + d ) = 1993
=> 1000a + 100b + 10c + d + a + b + c + d =1993
=> 1001a + 101b + 11c + 2d = 1993
Vì 0 < a \(\le\)9
=> a = 1
=> 101b + 11c + 2d = 992
Vì b là chữ số
+ Nếu b \(\le\)8
=> c,d không tồn tại
+ Nếu b = 9
=> 11c + 2d = 83
Vì c là chữ số
+ Nếu < 7
=> d không tồn tại
+ Nếu c >
=> 11c > 83
+ Nếu c = 7
=> 2d = 6
=> d = 3
Vậy số cần tìm là: 1973
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm một số có 3 chữ số biết rằng nếu lấy số đó chia cho tổng các chữ số của nó thì vừa hết và lấy số đó cộng với 129 thì được số mới có 3 chữ số giống nhau
Tìm số tự nhiên có 2 chữ số biết rằng nếu lấy số đó cộng với tổng các chữ số của nó thì được kết quả là 80
Gọi số đó là ab \(\left(a\ne0\right)\), (a,b là chữ số)
Ta có: ab + a+b =80 <=> 10a+b+a+b=80 <=> 11a+2b=80
Vì \(b\le9\Rightarrow2b\le18\Rightarrow11a\ge62\Rightarrow a\ge6\)
Mà ta có 11a+2b=80, 2b chia hết cho 2, 80 chia hết cho 2 => 11a chia hết cho 2 => a chia hết cho 2
=> a=6 hoặc a=8
Nếu a=6 thì b=7 => số đó là 67.
Nếu a=8 thì b=-4 (loại)
Vậy số đó là 67
Đúng 0
Bình luận (0)
1.Tìm số tự nhiên có 2 chữ số biết rằng lấy tổng các chữ số của nó cộng với tích các chữ số của nó thì bằng chính nó.2.Tìm số tự nhiên có 3 chữ số biết rằng số đó gấp 11 lần tổng các chữ số của nó.3.Hiệu 2 số là 57. Số bị trừ có chữ số hàng đơn vị là 3. Nếu gạch bỏ chữ số hàng đơn vị của số bị trừ thì ta được số trừ. Tìm số bị trừ và số trừ.
Đọc tiếp
1.Tìm số tự nhiên có 2 chữ số biết rằng lấy tổng các chữ số của nó cộng với tích các chữ số của nó thì bằng chính nó.
2.Tìm số tự nhiên có 3 chữ số biết rằng số đó gấp 11 lần tổng các chữ số của nó.
3.Hiệu 2 số là 57. Số bị trừ có chữ số hàng đơn vị là 3. Nếu gạch bỏ chữ số hàng đơn vị của số bị trừ thì ta được số trừ. Tìm số bị trừ và số trừ.
1.19
2.198
3.SBT: 63, ST: 6
Nếu lấy một số có hai chữ số chia cho tích hai chữ số của nó thì được thương là 2 và dư là 18. Nếu lấy tổng bình phương các chữ số của số đó cộng với 9 thì được số đã cho. Hãy tìm số đó.
Gọi a là chữ số hàng chục, b là chữ số hàng đơn vị. Điều kiện a, b nguyên 1 ≤ a ≤ 9 và 0 ≤ b ≤ 9. Ta có:
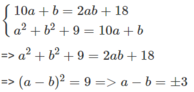 '
'
Trường hợp 1
a - b = 3 ⇒ a = b + 3
Thay vào phương trình đầu của hệ phương trình ta được:
11b + 30 = 2(b + 3)b + 18 ⇒ 2 b 2 - 5 b + 12 = 0
Phương trình cuối có hai nghiệm: b 1 = 4 , b 2 = -3/2
Giá trị b 2 = -3/2 không thỏa mãn điều kiện 0 ≤ b ≤ 9 nên nên bị loại.
Vậy b = 4, suy ra a = 7.
Trường hợp 2
a - b = - 3 ⇒ a = b - 3
Thay vào phương trình của hệ phương trình ra được
11b - 30 = 2(b - 3)b + 18 ⇒ 2 b 2 - 17 b + 48 = 0
Phương trình này vô nghiệm.
Vậy số phải tìm là 74.
Đúng 0
Bình luận (0)
Nếu lấy một số có hai chữ số chia cho tích hai chữ số của nó thì được thương là 2 và dư là 18. Nếu lấy tổng bình phương các chữ số của số đó cộng với 9 thì được số đã cho. Hãy tìm số đó ?
Gọi số cần tìm có dạng: \(\overline{ab}\) \(\left(a,b\in N;a,b>0\right)\)
Thương của số cần tìm với tích hai chữ số của nó có dạng:\(\overline{ab}:\left(ab\right)\).
Theo giả thiết ta có: \(\overline{ab}=2ab+18\).
Tổng bình phương các chữ số của số cần tìm là: \(a^2+b^2+9=\overline{ab}\).
Ta có hệ phương trình: \(\left\{{}\begin{matrix}2ab+18=\overline{ab}\\a^2+b^2+9=\overline{ab}\end{matrix}\right.\)\(\Rightarrow a^2+b^2+9=2ab+18\)\(\Leftrightarrow\left(a-b\right)^2=9\)\(\Leftrightarrow\left|a-b\right|=3\).
Th 1. \(a-b=3\)\(\Leftrightarrow a=b+3\). Khi đó:
\(2ab+18=\overline{ab}\)\(\Leftrightarrow2ab+18=10a+b\)\(\Leftrightarrow2\left(b+3\right)b+18=10\left(b+3\right)+b\)\(\Leftrightarrow2b^2-5b-12=0\)\(\Leftrightarrow\left\{{}\begin{matrix}b=4\left(tm\right)\\b=\dfrac{-3}{2}\left(l\right)\end{matrix}\right.\).
Với \(b=4\) ta có \(a=3+b=3+4=7\). Vậy số đó là 73.
Th2: \(a-b=-3\)\(\Leftrightarrow a=b-3\). Khi đó:
\(2ab+18=10a+b\)\(\Leftrightarrow2\left(b-3\right)b+18=10\left(b-3\right)+b\)
\(\Leftrightarrow2b^2-17b+48=0\) (Vô nghiệm).
Vậy số cần tìm là: 73.
Đúng 0
Bình luận (0)
Tìm số có 3 chữ số , biết rằng nếu đem cộng số đó với tổng các chữ số của nó thì được 555
tìm một số có 2chữ số giống nhau,biết rang nếu lấy số đó cộng vói tổng các chữ số của nó thì được kết quả là52
Đúng 0
Bình luận (0)






















