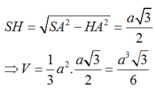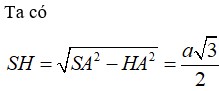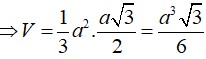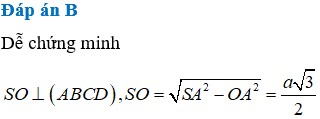Tính thể tích SABCD biết SABCD là h/c đều có tất cả các cạnh = a

Những câu hỏi liên quan
Tính VSABCD�Δ���� biết SABCD là h/c đều có tất cả các cạnh a
Đọc tiếp
Tính biết SABCD là h/c đều có tất cả các cạnh = a
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ACBD\right)\)
\(AC=AB\sqrt{2}=a\sqrt{2}\Rightarrow AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
Pitago tam giác vuông SAO:
\(SO=\sqrt{SA^2-AO^2}=\sqrt{a^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{2}}{2}.a^2=\dfrac{a^3\sqrt{2}}{6}\)
Đúng 1
Bình luận (0)
Hình chóp SABCD, đáy ABCD là hình thoi,
∆
BCD là
∆
đều cạnh a, tâm H. Biết SH
⊥
(ABCD) và
∆
SAC vuông tại S. Tính thể tích V của SABCD. A. V
a
3
3
4
B. V
a
3
2
6
C. V...
Đọc tiếp
Hình chóp SABCD, đáy ABCD là hình thoi, ∆ BCD là ∆ đều cạnh a, tâm H. Biết SH ⊥ (ABCD) và ∆ SAC vuông tại S. Tính thể tích V của SABCD.
A. V = a 3 3 4
B. V = a 3 2 6
C. V = a 3 3 3
D. V = a 3 3
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm sao cho
A
S
¯
B
G
¯
. Thể tích của khối đa diện SABCD là A.
a
3
2
12
B. ...
Đọc tiếp
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm sao cho A S ¯ = B G ¯ . Thể tích của khối đa diện SABCD là
A. a 3 2 12
B. a 3 2 24
C. 5 a 3 2 36
D. 3 a 3 2 24
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm đối xứng của G mặt phẳng (ABC). Thể tích khối đa diện SABCD là: A.
a
3
2
B.
a
3
2
3
C.
a
3
2
6...
Đọc tiếp
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm đối xứng của G mặt phẳng (ABC). Thể tích khối đa diện SABCD là:
A. a 3 2
B. a 3 2 3
C. a 3 2 6
D. a 3 2 9
Cho hình chóp đều sabcd có cạnh đáy bằng a góc giữa mặt bên và đáy là 60 độ tính thể tích sabcd
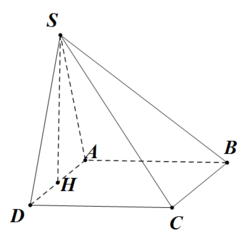
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABCD.
Đọc tiếp
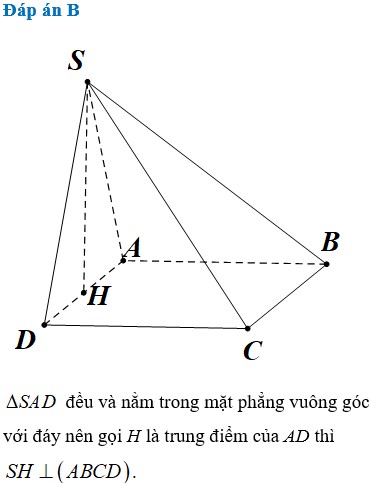
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABCD.
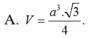
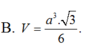
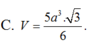
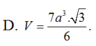
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABCD A.
V
a
3
3
4
B.
V
a
3
3
6
C.
V...
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp SABCD
A. V = a 3 3 4
B. V = a 3 3 6
C. V = 5 a 3 3 6
D. V = 7 a 3 3 6
Cho hình chóp SABCD có đáy là hình chữ nhật tâm O với AB2a, BCa. Các cạnh bên của hình chóp đều bằng nhau và bằng
a
2
. Thể tích hình chóp SABCD bằng A.
a
3
3
2
B.
a
3
3
3
C. ...
Đọc tiếp
Cho hình chóp SABCD có đáy là hình chữ nhật tâm O với AB=2a, BC=a. Các cạnh bên của hình chóp đều bằng nhau và bằng a 2 . Thể tích hình chóp SABCD bằng
A. a 3 3 2
B. a 3 3 3
C. a 3 3 4
D. a 3 3 5
Tính thể tích SABC biết SABC là h/c đều có tất cả các cạnh = a
Gọi H là trung điểm của BC, O là trọng tâm của ΔABC
ΔABC đều có O là trọng tâm
nên OA=OB=OC
mà SA=SB=SC
nên SO⊥(ABC)
Xét ΔABC đều có AH là đường trung tuyến
nên \(AH=BC\cdot\frac{\sqrt3}{2}=\frac{a\sqrt3}{2}\)
Xét ΔABC có
AH là đường trung tuyến
O là trọng tâm
Do đó: A,O,H thẳng hàng
=>\(AO=\frac23AH=\frac23\cdot\frac{a\sqrt3}{2}=\frac{a\sqrt3}{3}\)
ΔSOA vuông tại O
=>\(SO^2+OA^2=SA^2\)
=>\(SO^2=a^2-\left(\frac{a\sqrt3}{3}\right)^2=a^2-a^2\cdot\frac39=\frac69a^2\)
=>\(SO=\frac{a\sqrt6}{3}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\frac{AB^2\sqrt3}{4}=\frac{a^2\sqrt3}{4}\)
Thể tích hình chóp S.ABC là:
\(V=\frac13\cdot SO\cdot S_{ABC}=\frac13\cdot\frac{a\sqrt6}{3}\cdot\frac{a^2\sqrt3}{4}=\frac{a^3\cdot3\sqrt2}{36}=\frac{a^3\sqrt2}{18}\)
Đúng 0
Bình luận (0)