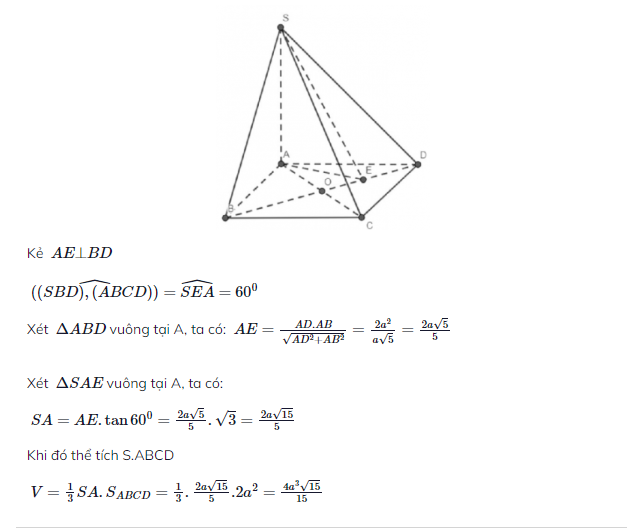
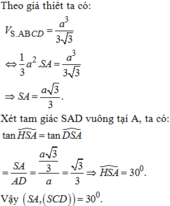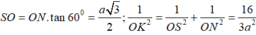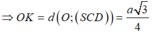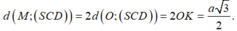Tính VS.ABCD biết S.ABCD là k/c đều có cạnh đáy a, góc giữa cạnh bên và đáy 60o

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA2a. Góc giữa (SAB) và đáy bằng 60o, góc giữa (SBC) và đáy bằng 45o. Tính thể tích khối chóp S.ABCD biết chân đường cao hạ từ S nằm trong hình vuông ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA=2a. Góc giữa (SAB) và đáy bằng 60o, góc giữa (SBC) và đáy bằng 45o. Tính thể tích khối chóp S.ABCD biết chân đường cao hạ từ S nằm trong hình vuông ABCD.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA2a. Góc giữa (SAB) và đáy bằng
60
o
, góc giữa (SBC) và đáy bằng
45
o
. Tính thể tích khối chóp S.ABCD biết chân đường cao hạ từ S nằm trong hình vuông ABCD. A.
16
a
3
7
dvtt
B.
16...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA=2a. Góc giữa (SAB) và đáy bằng 60 o , góc giữa (SBC) và đáy bằng 45 o . Tính thể tích khối chóp S.ABCD biết chân đường cao hạ từ S nằm trong hình vuông ABCD.
A. 16 a 3 7 dvtt
B. 16 a 3 21 dvtt
C. 2 a 3 ( dvtt )
D. 2 a 3 dvtt
1. cho h/c đều SABCD có AB=a. Góc giữa cạnh bên và mặt đáy=45o . Tính VS.ABCD
Gọi O là tâm của hình vuông ABCD
Vì S.ABCD là hình chóp đều và O là tâm của đáy
nên SO\(\perp\)(ABCD)
Góc giữa cạnh bên và mặt đáy là 45 độ
=>\(\widehat{SA;\left(ABCD\right)}=45^0\)
=>\(\widehat{AS;AO}=45^0\)
=>\(\widehat{SAO}=45^0\)
ABCD là hình vuông
=>\(AC=AB\cdot\sqrt{2}=a\sqrt{2}\)
O là tâm của hình vuông ABCD
=>O là trung điểm của AC
=>\(AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
Xét ΔSOA vuông tại O có \(tanSAO=\dfrac{SO}{OA}\)
=>\(\dfrac{SO}{\dfrac{a\sqrt{2}}{2}}=1\)
=>\(SO=\dfrac{a\sqrt{2}}{2}\)
Thể tích hình chóp S.ABCD là:
\(V=\dfrac{1}{3}\cdot SO\cdot S_{ABCD}=\dfrac{1}{3}\cdot\dfrac{a\sqrt{2}}{2}\cdot a^2=\dfrac{a^3\cdot\sqrt{2}}{6}\)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác cân tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy là 60o. Tính thể tích khối chóp S.ABCD A.
a
3
5
B.
a
3
5
3
C....
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác cân tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy là 60o. Tính thể tích khối chóp S.ABCD
A. a 3 5
B. a 3 5 3
C. a 3 3 6
D. a 3 15 6
Đáp án D
Gọi H là trung điểm của AD, khi đó từ giả thiết ta có SH ⊥ (ABCD). Ta có:

Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, biết
V
S
.
A
B
C
D
a
3
3
3
....
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, biết V S . A B C D = a 3 3 3 . Tính góc giữa SA và mặt phẳng (SCD).
A. 60 0 .
B. 45 0 .
C. 30 0 .
D. 90 0 .
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, biết
V
S
.
A
B
C
D
a
3
3
3
. Tính góc giữa SA và mặt phẳng (SCD). A. 60
°
B. 45
°
C...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, biết V S . A B C D = a 3 3 3 . Tính góc giữa SA và mặt phẳng (SCD).
A. 60 °
B. 45 °
C. 30 °
D. 90 °
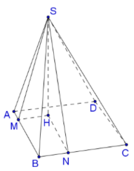
Chọn C.
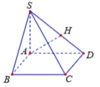
Ta có: 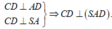
Kẻ AH
⊥
SD, suy ra 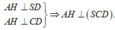
Từ đây ta có: SH là hình chiếu của SA lên (SCD).
Do đó: ![]()
Theo giả thiết ta có:
Xét tam giác SAD vuông tại A, ta có:
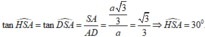
Vậy ![]()
Đúng 0
Bình luận (0)
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là
60
o
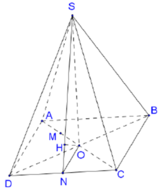
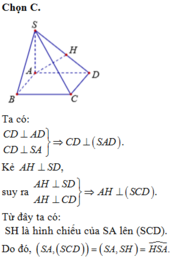
. Tính khoảng cách từ điểm B đến mặt phẳng (SCD).
Đọc tiếp
Cho hình chóp đều S.ABCD, cạnh đáy bằng a, góc giữa mặt bên và mặt đáy là 60 o . Tính khoảng cách từ điểm B đến mặt phẳng (SCD).
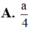
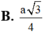
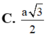
câu 1 : cho hình chóp S.ABCD có đáy ABCD là HCN AB = a ; AD = 2a ; cạnh bên SA vuông góc với đáy . tính thể tích V của khối chóp S.ABCD biết góc giữa 2 mặt phẳng (SBD) và (ABCD) = 60o
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc ABC bằng , cạnh bên SA vuông góc với đáy, SC tạo với đáy góc
60
o
. Tính thể tích khối chóp S.ABCD. A.
a
3
2
B.
a
3
3
C.
a
3
5
D.
a...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc ABC bằng , cạnh bên SA vuông góc với đáy, SC tạo với đáy góc 60 o . Tính thể tích khối chóp S.ABCD.
A. a 3 2
B. a 3 3
C. a 3 5
D. a 3 2 2
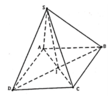
Ta có:
A C = a ⇒ S A = A C tan 60 o = a 3 B D = 2 B I = 2 . B C . sin 60 o = a 3 V = 1 3 S A . S A B C D = 1 3 . S A . 1 2 . A C . B D
Đáp án A
Đúng 0
Bình luận (0)