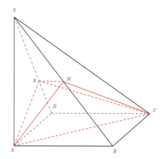
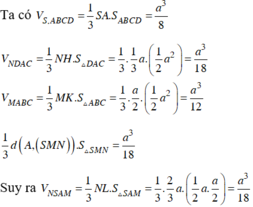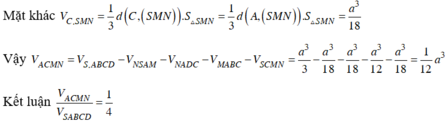Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi E là trung điểm của BC, F là điểm thuộc cạnh CD sao cho \(\widehat{EAF}=45^0\) và G thuộc cạnh SA. Biết FG //(SBC). Khi đó tỉ số \(\dfrac{GA}{GS}\) là

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAa và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN2ND. Tính tỉ số thể tích
V
A
C
M
N
V
S
A
B
C
D
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN=2ND. Tính tỉ số thể tích V A C M N V S A B C D
![]()
![]()
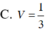
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN 2ND. Tính tỉ số thể tích
V
A
C
M
N
V
S
A
B
C
D
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN = 2ND. Tính tỉ số thể tích V A C M N V S A B C D
Cho hình chóp S.ABCD. có đáy ABCD là hình bình hành, E là trung điểm của SA, F, G lần lượt là các điểm thuộc cạnh BC, CD
C
F
F
B
;
G
C
G
D
. Thiết diện của hình chóp cắt bởi
E
F
G...
Đọc tiếp
Cho hình chóp S.ABCD. có đáy ABCD là hình bình hành, E là trung điểm của SA, F, G lần lượt là các điểm thuộc cạnh BC, CD C F < F B ; G C < G D . Thiết diện của hình chóp cắt bởi E F G là
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
Chọn C.
Phương pháp : Dựng thiết diện.
Cách giải : Gọi I, J lần lượt là giao điểm của GF với AB và AD.
Gọi H là giao điểm của IE và SB.
Gọi K là giao điểm của SD và EJ.
Suy ra thiết diện cần tìm là ngũ giác EHFGK.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, E là trung điểm của SA, F, G lần lượt là các điểm thuộc cạnh BC, CD (CF<FB; GC<GD). Thiết diện của hình chóp cắt bởi (EFG) là :
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
Chọn đáp án C
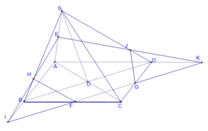
Trong mp (ABCD), gọi

Do đó ngũ giác EHFGJ là thiết diện của hình chóp cắt bởi (EFG)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm 0; cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm của SD và BC. Tính khoảng cách từ điểm M đến mặt phẳng (SBC)
Cho hình chóp S.ABCD có đáy abcd là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CD, SD
1. Xác định giao tuyến của (SAC) ; (SBD) và chứng minh NP song song với (SBC)
2.Gọi Q là giao điểm của SA với (MNP). Tính tỉ số \(\dfrac{SQ}{SA}\)
1: Gọi giao điểm của AC và BD là O trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SO
Xét ΔSDC có
P,N lần lượt là trung điểm của DS,DC
=>PN là đường trung bình của ΔSDC
=>PN//SC
PN//SC
SC\(\subset\)(SBC)
PN không nằm trong mp(SBC)
Do đó: PN//(SBC)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy abcd là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CD, SD
1. Xác định giao tuyến của (SAC) ; (SBD) và chứng minh NP song song với (SBC)
2.Gọi Q là giao điểm của SA với (MNP). Tính tỉ số \(\dfrac{SQ}{SA}\)
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành , có tất cả các cạnh bằng a. Gọi E, F lần lượt là trung điểm của SA, SB Gọi M là một điểm thuộc cạnh BC sao cho BM = 2MC.
a, Chứng minh AB // (MEF)
b, Xác định thiết diện của hình chóp bị cắt bởi mặt phẳng (MEF) và tính diện tích thiết diện
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là trung điểm của cạnh SA, F, G là các điểm thuộc cạnh SC, AB (F không là trung điểm của SC). Thiết diện của hình chóp cắt bởi mặt phẳng (EFG) là: A. Lục giác B. Tứ giác C. Ngũ giác D. Tam giác
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là trung điểm của cạnh SA, F, G là các điểm thuộc cạnh SC, AB (F không là trung điểm của SC). Thiết diện của hình chóp cắt bởi mặt phẳng (EFG) là:
A. Lục giác
B. Tứ giác
C. Ngũ giác
D. Tam giác
Đáp án C
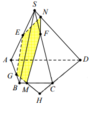
Kẻ EG cắt SB tại I, nối FI cắt BC tại M.
Kẻ GM cắt CD tại H, nối FH cắt SD tại N
Vậy thiết diện cần tìm là ngũ giác GMFNE (hình vẽ bên)
Đúng 0
Bình luận (0)