cho tam giác abc có ab = ac. gọi i là trung điểm của bc. cho góc b = 70 độ. trên tia đối ia lấy m sao cho im = ia. gọi k là trung điểm ab. tren tia đối km lấy n sao cho km = kn. kc cắt ai tại d. chứng minh cd = 2. kd

Những câu hỏi liên quan
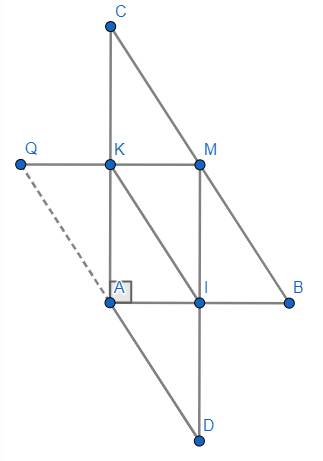
Cho ABC vuông tại A, (AB < AC) , gọi M là trung điểm của BC. I là trung điểm của AB, K là trung điểm của AC. Trên tia đối của tia IM lấy điểm D sao cho IM=ID. Trên tia đối của tia KM, lấy điểm Q sao cho KM=KQ.a. Cm: Tứ giác ADMC là hình bình hànhb. Cm: AIMK là hình chữ nhật (tứ giác có ba góc vuông là hình chữ nhật)c. Cm: D,A,Q thẳng hàng
Xem chi tiết
(a) \(I,M\) là trung điểm của \(AB,BC\Rightarrow IM\) là đường trung bình của \(\Delta ABC\Rightarrow\left\{{}\begin{matrix}IM\left|\right|AC\Leftrightarrow MD\left|\right|AC\left(1\right)\\IM=\dfrac{1}{2}AC\end{matrix}\right.\)
Lại có: \(IM=ID\Rightarrow MD=2IM=2\cdot\dfrac{1}{2}AC=AC\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow ADMC\) là hình bình hành (điều phải chứng minh).
(b) \(\left\{{}\begin{matrix}MI\left|\right|AC\left(cmt\right)\\AC\perp AB\left(gt\right)\end{matrix}\right.\Rightarrow MI\perp AB\Rightarrow\hat{AIM}=90^o\left(3\right)\).
\(M,K\) là trung điểm của \(BC,AC\Rightarrow MK\) là đường trung bình của \(\Delta ABC\Rightarrow MK\left|\right|AB\), mà \(AB\perp AC\left(gt\right)\Rightarrow MK\perp AC\Rightarrow\hat{AKM}=90^o\left(4\right)\).
Ta cũng có: \(\hat{A}=90^o\left(5\right)\).
Từ \(\left(3\right),\left(4\right),\left(5\right)\Rightarrow AIMK\) là hình chữ nhật (điều phải chứng minh).
(c) Do \(AIMK\) là hình chữ nhật (chứng minh trên) nên \(\left\{{}\begin{matrix}AK\left|\right|MI\Leftrightarrow AK\left|\right|ID\\AK=MI=ID\end{matrix}\right.\Rightarrow AKID\) là hình bình hành \(\Rightarrow IK\left|\right|AD\left(6\right)\).
Lại có: \(I,K\) là trung điểm của \(MD,MQ\Rightarrow IK\) là đường trung bình của \(\Delta MQD\Rightarrow IK\left|\right|QD\left(7\right)\)
Từ \(\left(6\right),\left(7\right)\Rightarrow Q,A,D\) thẳng hàng (điều phải chứng minh).
Đúng 1
Bình luận (0)
Bài 12: Cho tam giác ABC có AB AC. Trên tia đối của tia CA lấy điểm D sao cho CD AB. Gọi H, K lần lượt là trung điểm của AD, BC. Trung trực AD, BC cắt nhau tại I. Vẽ IE vuông góc với AB tại E.a) Chứng minh : IB IC; IA ID.b) Chứng minh: và AI là phân giác của góc BAC.c) Chứng minh: BE HC và AI là đường trung trực của đoạn thẳng EH.d) Từ C kẻ đường thẳng song song với AB, cắt đường thẳng EH tại F. Chứng minh: và E, K, F thẳng hàng.
Đọc tiếp
Bài 12: Cho tam giác ABC có AB < AC. Trên tia đối của tia CA lấy điểm D sao cho CD = AB. Gọi H, K lần lượt là trung điểm của AD, BC. Trung trực AD, BC cắt nhau tại I. Vẽ IE vuông góc với AB tại E.
a) Chứng minh : IB = IC; IA = ID.
b) Chứng minh: và AI là phân giác của góc BAC.
c) Chứng minh: BE = HC và AI là đường trung trực của đoạn thẳng EH.
d) Từ C kẻ đường thẳng song song với AB, cắt đường thẳng EH tại F. Chứng minh: và E, K, F thẳng hàng.
cho tam giác ABC vuông tại A có góc B=góc2C
a. tính góc B, C:
b. gọi I là trung điểm của BC, trên tia đối của tia IA lấy điểm D sao cho ID=IA. chứng minh: AB=DC
c. chứng minh: DC vuông góc AC
a: \(\widehat{B}=60^0;\widehat{C}=30^0\)
Đúng 0
Bình luận (1)
Cho tam giác ABC Gọi K là trung điểm của AB và E là trung điểm của AC.
Trên tia đối của tia CK lấy điểm M sao cho KM = KC.
Trên tia đối của EB lấy điểm N sao cho EN = EB.
a) Chứng minh AM =AN.
b) Chứng minh KM//BC; KN//BC
c) Chứng minh M,A,N thẳng hàng
Bài làm
~ Mik nghĩ pk là tia đối của KC mới chứng minh được, Và câu b mik nghĩ đề không đúng đâu, nhìn hình mik vẽ thì chắc bbạn cũnng hiểu. ~
Xét tam giác AKM và tam giác BKC có:
AK = BK (K trung điểm AB)
\(\widehat{AKM}=\widehat{BKC}\)( hai góc đối )
MK = KC ( gt )
=> Tam giác AKM = tam giác BKC ( c.g.c )
=> AM = BC (1)
Xét tam giác AEN và tam giác CEB có:
AE = EC ( E trung điểm AC )
\(\widehat{AEN}=\widehat{CEB}\)( hai góc đối )
EN = EB ( gt )
=> Tam giác AEN = tam giác CEB ( c.g.c )
=> AN = BC (2)
Từ (1) và (2) => AM = AN ( đpcm )
b) ~ Mik nghĩ là chứng minh AM // BC và AN // BC vì theo như hình mik vẽ thì thấy AM và AN cùng // BC. nếu k phải thì nói lại cho mik để mik làm lại cho ~
Vì tam giác AKM = tam giác BKC ( cmt )
=> \(\widehat{AMK}=\widehat{KCB}\)( hai góc tương ứng )
Mà hai góc này vị trí so le trong
=> AM // BC (3)
Vì tam giác AEN = tam giác CEB ( cmt )
=> \(\widehat{ANE}=\widehat{EBC}\)( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong.
=> AN // BC. (4)
c) Từ (3) và (4) => A, M, N thẳng hàng ( Theo tiên đờ Ơ-clit ) ( đpcm )
cho tam giác ABC gọi I là trung điểm của BC, biết rằng AI vuông góc với BC
a). Chứng minh: tam giác ABI = tam giác ACI
b). Chứng minh: tam giác ABC cân tại A
c). Trên tia đối của tia IA lấy điểm D sao cho ID = IA. Chứng minh: AB // CD
a: Xét ΔABI vuông tại I và ΔACI vuông tại I có
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Ta có: ΔABI=ΔACI
nên AB=AC
hay ΔABC cân tại A
c: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó:ABDC là hình bình hành
Suy ra: AB//CD
Đúng 2
Bình luận (2)
Bài 1: cho tam giác ABC gọi K,D lần lượt là trung điểm của AB,BC : trên tia đối của tia DA lấy M sao cho DMDA, trên tia đối của KM lấy N sao cho KM KN. Chứng minh A là trung điểm của NC Bài 2: Cho tam giác ABC (ABAC) từ trung điểm M của BC kẻ đường vuông góc với tia phân giác của góc A cắt AB, AC và tia phân giác của góc A tại D,E,H. Chứng minh rằng BDCEBài 3: Cho tam giác ABC vẽ BH vuông góc với AC (H thuộc AC) gọi M là trung điểm của AC biết góc ABH góc HBM góc MBC. Tính các góc cn lại của tam...
Đọc tiếp
Bài 1: cho tam giác ABC gọi K,D lần lượt là trung điểm của AB,BC : trên tia đối của tia DA lấy M sao cho DM=DA, trên tia đối của KM lấy N sao cho KM= KN. Chứng minh A là trung điểm của NC
Bài 2: Cho tam giác ABC (AB<AC) từ trung điểm M của BC kẻ đường vuông góc với tia phân giác của góc A cắt AB, AC và tia phân giác của góc A tại D,E,H. Chứng minh rằng BD=CE
Bài 3: Cho tam giác ABC vẽ BH vuông góc với AC (H thuộc AC) gọi M là trung điểm của AC biết góc ABH= góc HBM= góc MBC. Tính các góc cn lại của tam giác ABC
GIÚP MK VỚI MK ĐANG GẤP
Cho mik hỏi bạn đã giải đc bào này chưa ak nếu bạn giải đc thì bạn cho mik xin cách làm của bài 1 ak
Mik cảm ơn
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi K,D lần lượt là trung điểm AB và BC. Trên tia đối tia DA lấy M sao cho DM=DA . Trên tia đối tia KM lấy N sao KN=KM, Chứng minh A là trung điểm NC
Cho tam giác ABC có số đo góc A=90 độ, gọi I là trung điểm của BC. Trên tia đối của tia IA lấy điểm M sao cho IM=IA
a) Chứng minh tam giác AIB = tam giác MIC
b) Chứng minh AB // CM
c) Chứng minh AI = 1/2 BC
cho tam giác ABC vuông tại A biết AB=3cm , AC=4cm, I là trung điểm của BC. Trên tia đối của tia IA lấy điểm M sao cho IA=IM.
a,tính độ dài đoạn AI
b,cm tứ giác ABMC là hình chữ nhật.
c,gọi D là điểm đối xứng của B qua A. tứ giác AMCD là hình gì? vì sao?
d,gọi G là giao điểm của DM và BC .cm rằng DM=3GM
a) \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\) (theo định lí Pythagore trong tam giác \(ABC\) vuông tại \(A\))
\(AI=\dfrac{1}{2}BC=2,5\left(cm\right)\).
b) Tứ giác \(ABMC\) có hai đường chéo \(AM,BC\) cắt nhau tại trung điểm mỗi đường nên \(ABMC\) là hình bình hành.
Mà có \(\widehat{BAC}=90^o\) do đó \(ABMC\) là hình chữ nhật.
c) Tứ giác \(AMCD\) có \(AD=AB=AM,AD//CM\) suy ra \(AMCD\) là hình bình hành.
d) Gọi \(K\) là giao điểm của \(DM\) và \(AC\).
Do \(AMCD\) là hình bình hành nên hai đường chéo \(DM,AC\) cắt nhau tại trung điểm \(K\) của mỗi đường.
Xét tam giác \(ACM\): hai đường trung tuyến \(CI,MK\) cắt nhau tại \(G\) nên \(G\) là trọng tâm tam giác \(ACM\) suy ra \(MG=\dfrac{2}{3}MK=\dfrac{2}{3}.\dfrac{1}{2}MD=\dfrac{1}{3}MD\)
\(\Leftrightarrow DM=3GM\).
Đúng 0
Bình luận (0)