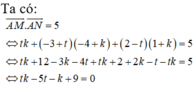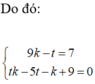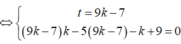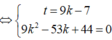Nếu đường thẳng d1: x+2y-11=0 cắt đường thẳng d2: 5x-3y-3=0 tại điểm M(x;y). Tìm giá trị căn bậc hai của x^2+y^2

Những câu hỏi liên quan
Cho ba đường thẳng
d
1
:
x
−
2
y
+
1
0
,
d
2
:
m
x
−
3
m
−
2
y
+
2
m
−
2
0
,
d
3
:
...
Đọc tiếp
Cho ba đường thẳng d 1 : x − 2 y + 1 = 0 , d 2 : m x − 3 m − 2 y + 2 m − 2 = 0 , d 3 : x + y − 5 = 0 . Giá trị m để hai đường thẳng d1;d2 cắt nhau tại một điểm nằm trên d3 là
A.m = 0
B.m = 1
C.m = 2
D. không tồn tại m thỏa mãn
Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng
d
1
:
x
-
1
1
y
+
1
1
z
-
3
-
1
;
d
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng d 1 : x - 1 1 = y + 1 1 = z - 3 - 1 ; d 2 : x - 1 1 = y + 2 1 = z - 2 1 . Viết phương trình đường thẳng d song song với mặt phẳng P : 2 x + 3 y + 4 z - 6 = 0 , cắt đường thẳng d 1 , d 2 lần lượt tại M và N sao cho A M → A N → = 5 và điểm N có hoành độ nguyên.
A. d : x - 2 1 = y - 2 = z - 2 1
B. d : x - 3 1 = y - 1 2 = z - 1 - 2
C. d : x 3 = y + 2 2 = z - 4 - 3
D. d : x - 1 4 = y + 1 - 4 = z - 3 1
Chọn B.
Phương pháp: Tham số hóa điểm M và N
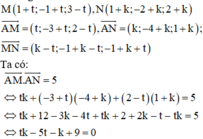

Do đó:

Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng
d
1
:
x
-
1
1
y
+
1
1
z
-
3
-
1
;
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng d 1 : x - 1 1 = y + 1 1 = z - 3 - 1 ; d 2 : x - 1 1 = y + 2 1 = z - 2 1 . Viết phương trình đường thẳng d song song với mặt phẳng (P):2x+3y+4z-6=0, cắt đường thẳng d1, d2 lần lượt tại M và N sao cho A M ⇀ . A N ⇀ = 5 và điểm N có hoành độ nguyên.
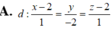
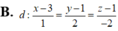
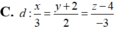
![]()
Trong mặt phẳng tọa độ Oxy cho điểm D(6;2) và hai đường thẳng (d1): x-2y+1=0; (d2): x+2y-3=0. Viết phương trình đường thẳng \(\left(\Delta\right)\) đi qua D và cắt hai đường thẳng (d1); (d2) tại hai điểm B; C sao cho tam giác tạo bởi ba đường thẳng (d1); (d2); \(\left(\Delta\right)\) là tam giác cân, với BC là cạnh đáy.
trên mặt phẳng tọa độ cho 2 đường thẳng (d1) : x-y+1=0, (d2) : x-3y-3=0 cắt nhau tại A. Hãy viết pt đường thẳng (d) đi qua M(1;1) sao cho (d1) cắt (d2) lần lượt tại tại B và C, Tam giác ABC vuông
Cho ba đường thẳng
d
1
:
3
x
−
4
y
+
1
0
,
d
2
:
5
x
+
3
y
−
1
0
,
d
3
:
x
+
y
+
6
0
. Số điểm M cách đều ba đường thẳng trên...
Đọc tiếp
Cho ba đường thẳng d 1 : 3 x − 4 y + 1 = 0 , d 2 : 5 x + 3 y − 1 = 0 , d 3 : x + y + 6 = 0 . Số điểm M cách đều ba đường thẳng trên là
A.1
B. 2
C.3
D. 4
Do các đường thẳng đôi một cắt nhau tại các điểm A, B, C nên các điểm cách đều các cạnh gồm tâm đường tròn nội tiếp và ba tâm đường tròn bàng tiếp.
Vậy có tất cả 4 điểm M cách đều ba đường thẳng đã cho.
đáp án D
Đúng 0
Bình luận (0)
Cho hai đường thẳng d1 : x+ 2y -1 0 và d2 : x- 3y +3 0. Phương trình đường thẳng d đối xứng với d1 qua là: A. x -3y- 2 0 B.x+ 3y+1 0 C. 3x-y1 0 D. x-3y+ 30
Đọc tiếp
Cho hai đường thẳng d1 : x+ 2y -1 = 0 và d2 : x- 3y +3 = 0. Phương trình đường thẳng d đối xứng với d1 qua là: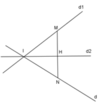
A. x -3y- 2= 0
B.x+ 3y+1= 0
C. 3x-y=1= 0
D. x-3y+ 3=0
Đáp án D
Gọi I là giao điểm của hai đường thẳng d1; d2 . Tọa độ điểm I là nghiệm của hệ:
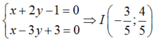
Lấy điểm m 1 ; 0 ∈ d 1 . Đường thẳng qua M và vuông góc với d2 có phương trình: 3x + y-3= 0
Gọi H = ∆ ∩ d 2 suy ra tọa độ điểm H là nghiệm của hệ:
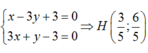
Phương trình đường thẳng
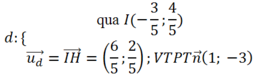
có dạng:
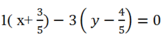
hay x-3y + 3= 0
Đúng 0
Bình luận (0)
Xét vị trí tương đối của các cặp đường thẳng sau. Nếu 2 đường thẳng giao nhau thì tìm giao điểm nếu có
a, (d1) 12x-6y+8=0 và (d2) 2x-y+3=0
b, (d2) x-2y+5=0 và (d3) 2x-3y=0
Viết phương trình đường thẳng d đối xứng qua d1 qua d2 biết d1:x+2y-1=0,d2 : x-3y+3=0
Gọi M là giao điểm \(d_1;d_2\Rightarrow\) tọa độ M thỏa mãn:
\(\left\{{}\begin{matrix}x+2y-1=0\\x-3y+3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\) \(\Rightarrow M\left(-\dfrac{3}{5};\dfrac{4}{5}\right)\)
Chọn \(N\left(1;0\right)\) là 1 điểm thuộc \(d_1\)
Gọi \(d_3\) là đường thẳng qua N và vuông góc \(d_2\Rightarrow d_3\) nhận (3;1) là 1 vtpt
Phương trình \(d_3\):
\(3\left(x-1\right)+1\left(y-0\right)=0\Leftrightarrow3x+y-3=0\)
Gọi P là giao điểm \(d_2;d_3\Rightarrow\) tọa độ P là nghiệm:
\(\left\{{}\begin{matrix}3x+y-3=0\\x-3y+3=0\\\end{matrix}\right.\) \(\Rightarrow P\left(\dfrac{3}{5};\dfrac{6}{5}\right)\)
Gọi Q là điểm đối xứng N qua \(d_2\Rightarrow P\) là trung điểm NQ
\(\Rightarrow\left\{{}\begin{matrix}x_Q=2x_P-x_N=\dfrac{1}{5}\\y_Q=2y_P-y_N=\dfrac{12}{5}\end{matrix}\right.\) \(\Rightarrow Q\left(\dfrac{1}{5};\dfrac{12}{5}\right)\)
\(\Rightarrow MQ\) đối xứng \(MN\) qua \(d_2\Rightarrow MQ\) là đường thẳng d cần tìm
\(\overrightarrow{MQ}=\left(\dfrac{4}{5};\dfrac{8}{5}\right)=\dfrac{4}{5}\left(1;2\right)\) \(\Rightarrow\) đường thẳng d nhận (2;-1) là 1 vtpt
Phương trình d:
\(2\left(x-\dfrac{1}{5}\right)-1\left(y-\dfrac{12}{5}\right)=0\Leftrightarrow2x-y+2=0\)
Đúng 3
Bình luận (0)