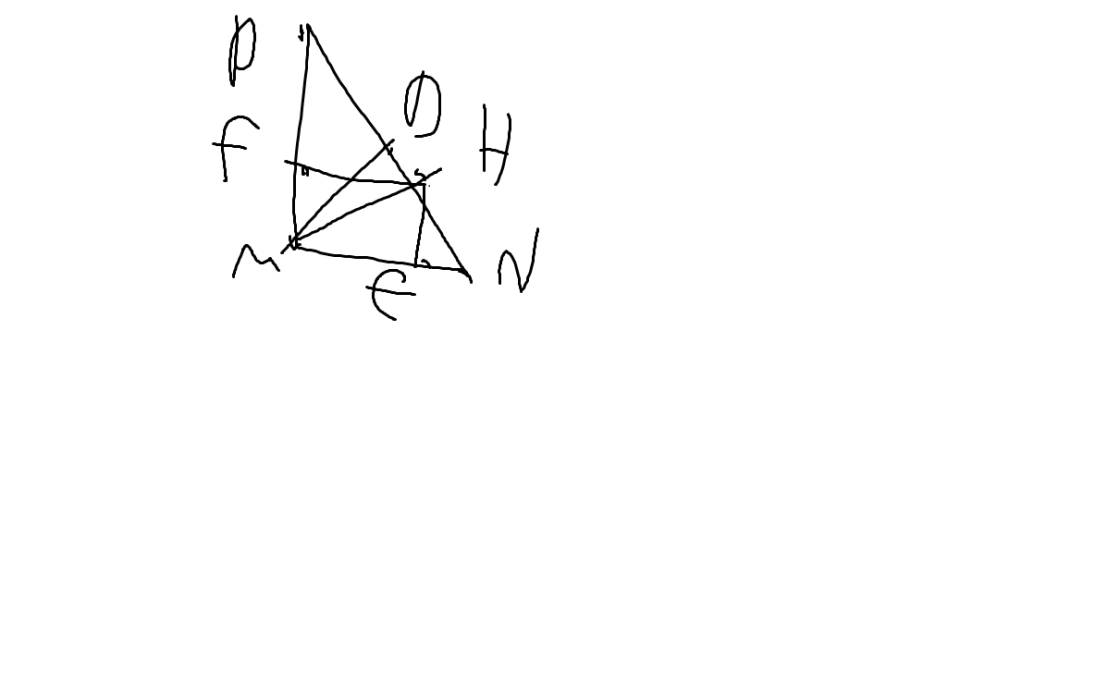1: Xét tứ giác ABOC có

\(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)

=>ABOC là tứ giác nội tiếp

=>A,B,O,C cùng thuộc một đường tròn

2: Xét (O) có

AB,AC là tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(1)

ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC tại trung điểm của BC

=>OA\(\perp\)BC tại H và H là trung điểm của BC

Xét ΔABO vuông tại B có BH là đường cao

nên \(AH\cdot AO=AB^2\left(3\right)\)

Xét (O) có

ΔBED nội tiếp

BD là đường kính

Do đó: ΔBED vuông tại E

=>BE\(\perp\)ED tại E

=>BE\(\perp\)AD tại E

Xét ΔDBA vuông tại B có BE là đường cao

nên \(AE\cdot AD=AB^2\left(4\right)\)

Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)

3: Xét ΔOKA vuông tại K và ΔOHF vuông tại H có

\(\widehat{KOA}\) chung

Do đó: ΔOKA đồng dạng với ΔOHF

=>\(\dfrac{OK}{OH}=\dfrac{OA}{OF}\)

=>\(OH\cdot OA=OK\cdot OF\left(5\right)\)

Xét ΔOCA vuông tại C có CH là đường cao

nên \(OH\cdot OA=OC^2=OD^2\left(6\right)\)

Từ (5) và (6) suy ra \(OK\cdot OF=OD^2\)

=>\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)

Xét ΔOKD và ΔODF có

\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)

\(\widehat{KOD}\) chung

Do đó: ΔOKD đồng dạng với ΔODF

=>\(\widehat{ODF}=\widehat{OKD}=90^0\)

=>FD là tiếp tuyến của (O;R)

a: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của BA(1)

Ta có: OB=OA

=>O nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra MO là đường trung trực của AB

=>MO\(\perp\)AB tại H và H là trung điểm của AB

b: Xét (O) có

ΔADE nội tiếp

AE là đường kính

Do đó: ΔADE vuông tại D

=>AD\(\perp\)DE tại D

=>AD\(\perp\)EM tại D

Xét ΔAEM vuông tại A có AD là đường cao

nên \(MD\cdot ME=MA^2\left(3\right)\)

Xét ΔMOA vuông tại A có AH là đường cao

nên \(MH\cdot MO=MA^2\left(4\right)\)

Từ (3) và (4) suy ra \(MD\cdot ME=MH\cdot MO\)

c: Ta có: ΔOED cân tại O

mà OF là đường trung tuyến

nên OF\(\perp\)ED tại F

Xét ΔOFM vuông tại F và ΔOHK vuông tại H có

\(\widehat{HOK}\) chung

Do đó: ΔOFM đồng dạng với ΔOHK

=>\(\dfrac{OF}{OH}=\dfrac{OM}{OK}\)

=>\(OF\cdot OK=OH\cdot OM\left(5\right)\)

Xét ΔOAM vuông tại A có AH là đường cao

nên \(OH\cdot OM=OA^2=OD^2\left(6\right)\)

Từ (5) và (6) suy ra \(OF\cdot OK=OD^2\)

=>\(\dfrac{OF}{OD}=\dfrac{OD}{OK}\)

Xét ΔOFD và ΔODK có

\(\dfrac{OF}{OD}=\dfrac{OD}{OK}\)

\(\widehat{FOD}\) chung

Do đó: ΔOFD đồng dạng với ΔODK

=>\(\widehat{OFD}=\widehat{ODK}=90^0\)

=>KD là tiếp tuyến của (O)

a: Xét (O) có

MA,MC là các tiếp tuyến

Do đó: MA=MC

=>M nằm trên đường trung trực của AC(1)

Ta có: OA=OC

=>O nằm trên đường trung trực của AC(2)

Từ (1) và (2) suy ra MO là đường trung trực của AC

=>MO\(\perp\)AC tại H và H là trung điểm của AC

Xét tứ giác MAOC có

\(\widehat{MAO}+\widehat{MCO}=90^0+90^0=180^0\)

=>MAOC là tứ giác nội tiếp

=>M,A,O,C cùng thuộc một đường tròn

b: Xét (O) có

ΔADB nội tiếp

AB là đường kính

Do đó: ΔADB vuông tại D

=>AD\(\perp\)DB tại D

=>AD\(\perp\)MB tại D

Xét ΔMAB vuông tại A có AD là đường cao

nên \(MD\cdot MB=MA^2\left(3\right)\)

Xét ΔMAO vuông tại A có AH là đường cao

nên \(MH\cdot MO=MA^2\left(4\right)\)

Từ (3) và (4) suy ra \(MD\cdot MB=MH\cdot MO\)

a: Xét tứ giác BCEF có

\(\widehat{BFC}=\widehat{BEC}=90^0\)

=>BCEF là tứ giác nội tiếp

=>B,C,E,F cùng thuộc một đường tròn

b: Xét tứ giác AEHF có

\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)

=>AEHF là tứ giác nội tiếp

=>A,E,H,F cùng thuộc một đường tròn

c: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có

\(\widehat{EAB}\) chung

Do đó: ΔAEB đồng dạng với ΔAFC

=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)

=>\(AE\cdot AC=AB\cdot AF\)

d: Xét (O) có

ΔABD nội tiếp

AD là đường kính

Do đó: ΔABD vuông tại B

=>AB\(\perp\)BD

Xét (O) có

ΔACD nội tiếp

AD là đường kính

Do đó: ΔACD vuông tại C

=>AC\(\perp\)CD

Ta có: BE\(\perp\)AC

CD\(\perp\)CA

Do đó: BE//CD

=>BH//CD

Ta có: CH\(\perp\)AB

BD\(\perp\)AB

Do đó: CH//BD

Xét tứ giác BHCD có

BH//CD

BD//CH

Do đó: BHCD là hình bình hành

=>BC cắt HD tại trung điểm của mỗi đường

mà M là trung điểm của BC

nên M là trung điểm của HD

Xét ΔDAH có

M,O lần lượt là trung điểm của DH,DA

=>MO là đường trung bình của ΔDAH

=>MO=AH/2

=>AH=2MO

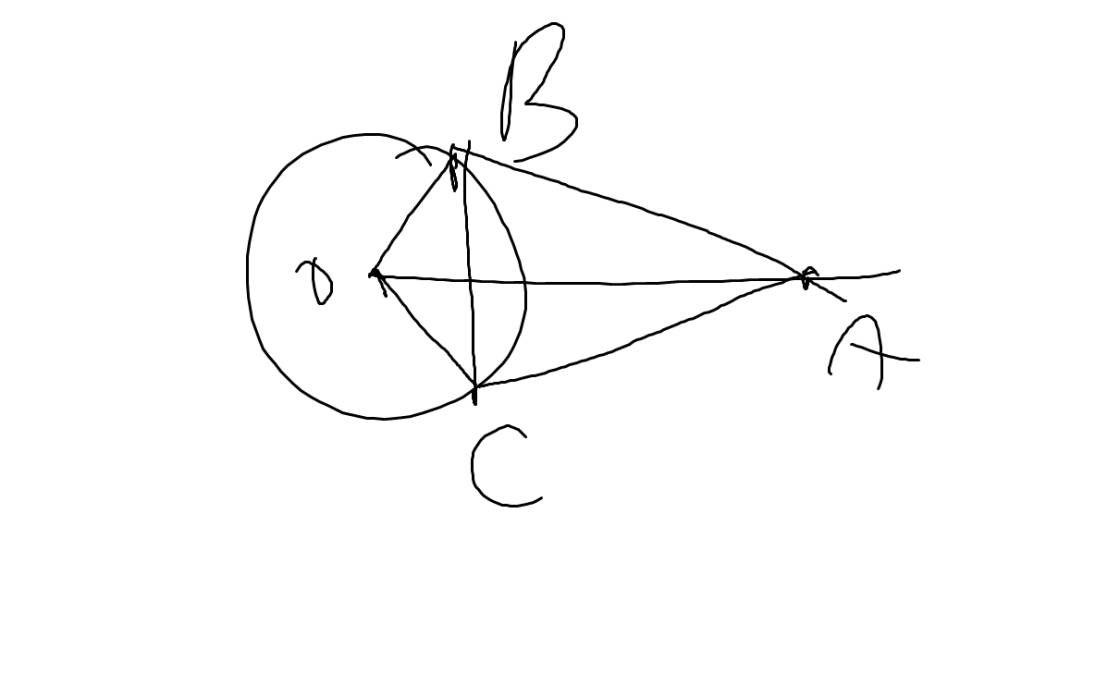
a: AB và AC là hai tiếp tuyến cắt nhau tại A

b: Xét tứ giác OBAC có

\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

=>OBAC là tứ giác nội tiếp

=>O,B,A,C cùng thuộc 1 đường tròn